TS Inter 2nd Year Maths 2B Solutions Chapter 8 Differential Equations Ex 8(b)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 8 Differential Equations Ex 8(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 8 Differential Equations Ex 8(b)

I.
Question 1.
Find the general solution of \(\sqrt{1-x^2} d y+\sqrt{1-y^2} d x\) = 0.
Solution:
Given equation is \(\sqrt{1-x^2} d y+\sqrt{1-y^2} d x\) = 0

⇒ sin^-1 y = – sin^-1 x + c
⇒ sin^-1 x + sin^-1 y + c is the general solution.

Question 2.
Find the general solution of \(\frac{d y}{d x}=\frac{2 y}{x}\).
?Solution:
The given equation can be written in variable separable form as \(\frac{d y}{d x}=\frac{2 y}{x}\).
⇒ \(\frac{\mathrm{dy}}{\mathrm{y}}=2\left(\frac{\mathrm{dx}}{x}\right)\)
⇒ log |y| = 2 log |x| + log c₁
⇒ log y = log x² + log c
⇒ log \(\left(\frac{y}{x^2}\right)\) = log c
⇒ y = cx²
⇒ x² = \(\frac{1}{c}\) y
⇒ x² = c₁y where c₁ is a constant is the general solution.

II. Solve the following differential equations.

Question 1.
\(\frac{d y}{d x}=\frac{1+y^2}{1+x^2}\)
Solution:
The given equation can be written in variable seperable form as
\(\frac{d y}{d x}=\frac{1+y^2}{1+x^2}\)
∴ \(\int \frac{d y}{1+y^2}=\int \frac{d x}{1+x^2}\)
⇒ tan^-1 y = tan^-1 x + tan^-1 c
⇒ tan^-1 y = tan^-1 x + tan^-1 c is the solution of the given differential equation.

Question 2.
\(\frac{d y}{d x}\) = e^y-x
Solution:
The given equation can be written in variable separable form as
\(\frac{d y}{d x}\) = e^y-x
⇒ \(\frac{d y}{e^y}=\frac{d x}{e^x}\)
⇒ ∫ e^-y dy = ∫ e^-x dx
⇒ – e^-y dy = – e^-x + c
⇒ e^-x – e^-y = c is the solution 0f the given differential equation.

Question 3.
(e^x + 1) y dy + (y + 1) dx = 0.
Solution:
The given differential equation can be written as (e^x + 1)y dy = – (y + 1) dx
⇒ \(\frac{y d y}{y+1}=-\frac{d x}{e^x+1}\)
⇒ \(\left[\frac{(y+1)-1}{y+1}\right] d y=\frac{-e^{-x}}{1+e^{-x}} d x\)
∴ ∫ dy – ∫ \(\frac{d y}{y+1}\) dx = ∫ \(\frac{\mathrm{e}^{-\mathrm{x}}}{1+\mathrm{e}^{-\mathrm{x}}}\) dx
⇒ y – log (y + 1) = log (1 + e^-x)
⇒ y = log (y + 1) + log (1 + e^-x) + log c
= log [(y + 1) (e^-x + 1) c]
∴ e^y = c(y + 1) (e^-x + 1)
∴ The solution of the given equation is
e^y = c (y + 1) (1 + e^-x).

Question 4.
\(\frac{d y}{d x}\) = e^x-y + x²e^-y
Solution:
\(\frac{d y}{d x}\) = e^x-y + x²e^-y
= e^-y (e^x + x²)
Writing in variable separable form we get
\(\frac{d y}{d x}\) = \(\frac{1}{y}\) (e^x + x²)
⇒ ∫ e^y dy = ∫ (e^x + x²) dx
⇒ e^y = e^x + \(\frac{x^3}{3}\) + c
The solution of the given equation is e^y = e^x + \(\frac{x^3}{3}\) + c.

Question 5.
tan y dx + tan x dy = 0.
Solution:
The given equation can be written as
\(\frac{d x}{\tan x}+\frac{d y}{\tan y}\) = 0
⇒ \(\int \frac{\mathrm{dx}}{\tan x}+\int \frac{\mathrm{dy}}{\tan y}\) = 0
⇒ ∫ cot x dx + ∫ cot y dy = 0
⇒ log (sin x) + log (sin y) = log c
⇒ sin x sin y = c is the solution of the given differential equation.

Question 6.
\(\sqrt{1+x^2} d x+\sqrt{1+y^2} d y\) = 0
Solution:
The given equation can be written in variable seperable form as

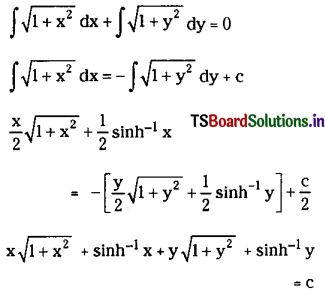
Question 7.
y – x\(\frac{d y}{d x}\) = 5 (y² + \(\frac{d y}{d x}\))
Solution:
The given differential equation is

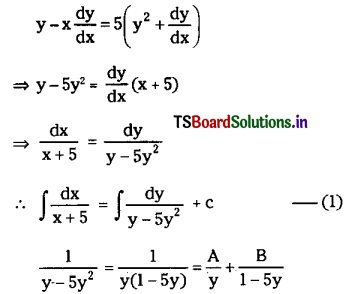
∴ 1 = A (1 – 5y) + By
⇒ A = 1 and B – 5A = 0
⇒ B = 5
∴ \(\int \frac{1}{y-5 y^2} d y=\int \frac{1}{y} d y+\int \frac{5}{1-5 y} d y\)
= log |y| – log (1 – 5y)
∴ From (1)
log |x + 5| = log |y| – log (1 – 5y) + log c
⇒ x + 5 = \(\frac{c y}{1-5 y}\)
∴ Solution of the given dillerential equation is 5 + x = \(\frac{c y}{1-5 y}\)

Question 8.
\(\frac{d y}{d x}=\frac{y(x+1)}{x(y+1)}\)
Solution:
The given equation \(\frac{d y}{d x}=\frac{y(x+1)}{x(y+1)}\) writing in variable separable form
\(\frac{(y+1) d y}{y}=\frac{(x+1) d x}{x}\)
\(\int\left(\frac{y+1}{y}\right) d y=\int \frac{(x+1) d x}{x}\)
⇒ y + log |y| = x + log |x| + log c
⇒ y – x = |og |x| – log |y| + log c
= log \(\left(\frac{c x}{y}\right)\)
∴ y – x = log \(\left(\frac{c x}{y}\right)\) is the solution.

III. Solve the following differential equations.

Question 1.
\(\frac{d y}{d x}=\frac{1+y^2}{\left(1+x^2\right) x y}\)
Solution:
The given equation is \(\frac{d y}{d x}=\frac{1+y^2}{\left(1+x^2\right) x y}\) which can be written in variable separable form as

⇒ (1 + x²) (1 + y²) = c²x²
= cx² where c² = c is a constant
∴ The solution of the given differential equation is
(1 + x²) (1 + y²) = cx²

Question 2.
\(\frac{d y}{d x}\) + x² = x² e^3y
Solution:
The given equation can be written in variable separable form as
\(\frac{d y}{d x}\) = x² e^3y – x²
= x² (e^3y – 1)
\(\frac{d y}{e^{3 y}-1}\) = xsup>2 dx
∴ ∫ \(\frac{d y}{e^{3 y}-1}\) = ∫ x² dx
⇒ ∫ \(\left(\frac{e^{-3 y}}{1-e^{-3 y}}\right)\) dy = \(\frac{x^3}{3}\) + c
⇒ log (1 – e^-3y) = x³ + c
⇒ 1 – e^-3y = e^x3 + e^c
= k e^x3
∴ The solution of the given differential equation is 1 – e^-3y = k e^x3.

Question 3.
(xy² + x) dx + (yx² + y) dy = 0
Solution:
The given dilferential equation can be written as
x (y² + 1) dx + y(x² + 1) dy = 0 which can be expressed in variable separable form as
\(\frac{1}{2} \int \frac{2 x d x}{x^2+1}+\frac{1}{2} \int \frac{2 y d y}{y^2+1}\) = 0
⇒ \(\frac{1}{2}\) log(x² + 1) + log (y² + 1) = log c
⇒ log \(\sqrt{\mathrm{x}^2+1}\) + log \(\sqrt{\mathrm{y}^2+1}\) = log c
⇒ (1 + x²) (1 + y²) = c².

Question 4.
\(\frac{d y}{d x}\) = 2y tanh x
Solution:
The given equation is \(\frac{d y}{d x}\) = 2y tanh x.
\(\frac{d y}{y}\) = 2 tanh x (variable separable form)
∫ \(\frac{d y}{y}\) = 2 ∫ tanh x dx
⇒ log y = 2 log |cosh x| + log c
= log |cosh² x| + log c
log y = log (c cosh² x)
y = c .cosh² x which is the solution of the given differential equation.

Question 5.
Sin^-1 (\(\frac{d y}{d x}\)) = x + y
Solution:
The given equation is Sin^-1 (\(\frac{d y}{d x}\)) = x + y
⇒ sin (x + y) = \(\frac{d y}{d x}\) …………..(1)

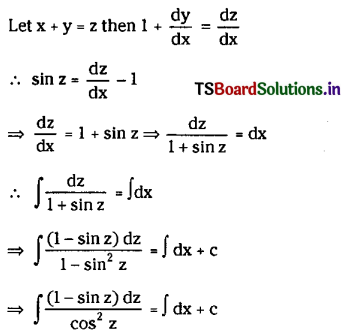
⇒ ∫ sec² dz – ∫ sec z tan x dx = ∫ dx + c
⇒ tan z – sec z = x + c
⇒ tan (x + y) – sec (x + y) = x + c is the solution of the given differential equation.

Question 6.
\(\frac{d y}{d x}+\frac{y^2+y+1}{x^2+x+1}\) = 0
Solution:
Given equation in variable separable form is
\(\frac{d y}{y^2+y+1}=-\frac{d x}{x^2+x+1}\)

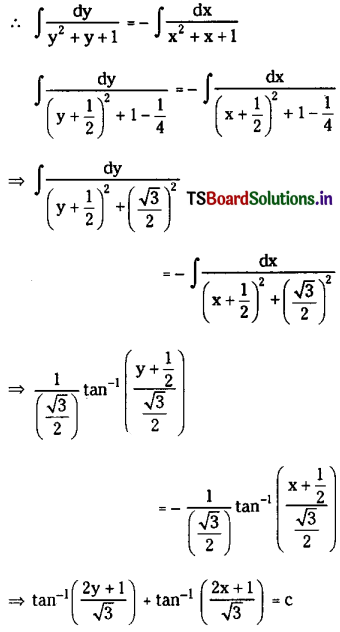
Question 7.
\(\frac{d y}{d x}\) = tan² (x + y)
Solution:
Let x + y = z then 1 + \(\frac{d y}{d x}\) = \(\frac{d z}{d x}\)
from the given equation
∴ 1 + \(\frac{d y}{d x}\) = 1 + tan² (x + y)
⇒ \(\frac{d z}{d x}\) = sec² z
⇒ ∫ \(\frac{\mathrm{d} z}{\sec ^2 z}\) = ∫ dx + c
⇒ ∫ cos² z dz = x + c
⇒ ∫ \(\left(\frac{1+\cos 2 z}{2}\right)\) dz = x + c
⇒ \(\frac{1}{2}\) z + \(\frac{1}{4}\) sin 2z = x + c
⇒ 2z + sin 2z = 4x + 4c
⇒ 2 (x + y) + sin 2 (x + y) = 4x + 4c
⇒ sin 2 (x + y) = 2x – 2y + 4c
= 2x – 2y + c₁
where c₁ = 4c.