TS Inter 2nd Year Maths 2B Solutions Chapter 7 Definite Integrals Ex 7(d)

Students must practice this TS Intermediate Maths 2B Solutions Chapter 7 Definite Integrals Ex 7(d) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2B Solutions Chapter 7 Definite Integrals Ex 7(d)

I. Find the area of the region enclosed by the given curves.

Question 1.
y = cos x, y = 1 – \(\frac{2 x}{\pi}\)
Solution:
Consider the graphs of the functions
f(x) = cos x and g(x) = 1 – \(\frac{2 x}{\pi}\)

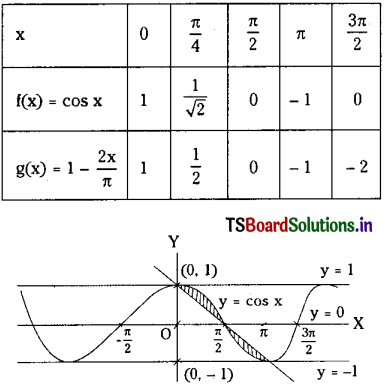
The two curves intersect at (\(\frac{\pi}{2}\), 0) and (π, -1)

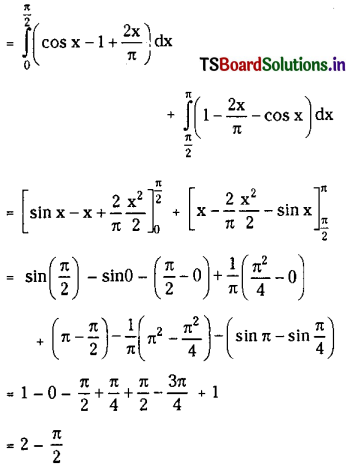
∴ The area enclosed between the curves y = cos x, y = 1 – \(\frac{2 \mathrm{x}}{\pi}\) is (2 – \(\frac{\pi}{2}\)).

Question 2.
y = cos x, y = sin 2x, x = 0, x = \(\frac{\pi}{2}\).
Solution:
Consider the graphs of the functions f(x) = cos x and g(x) = sin 2x.

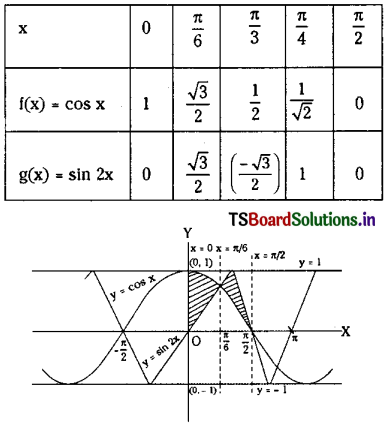
Taking f(x) = cos x and g(x) = sin 2x in [0, \(\frac{\pi}{6}\)]
we have f(x) ≥ g(x) and also in \(\left[\frac{\pi}{6}, \frac{\pi}{2}\right]\) have g(x) ≥ f(x).
Hence area enclosed between f(x) = cos x and g(x) = sin 2x is

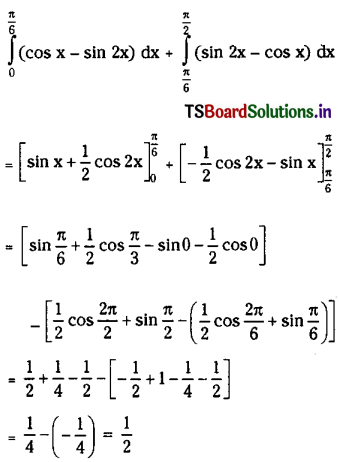
∴ Area enclosed between the curves y = cos x, y = sin 2x, x = 0, x = \(\frac{\pi}{2}\) is \(\frac{1}{2}\) sq.units.

Question 3.
y = x³ + 3, y = 0, x = – 1, x = 2. (Mar. ’12)
Solution:

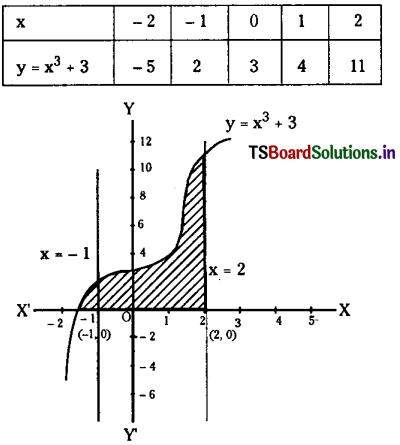
Required area enclosed between y = x³ + 3, y = 0, x = – 1, x = 2 is

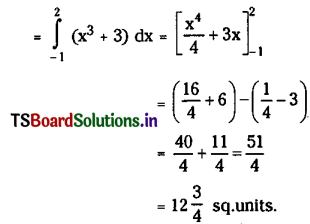
Question 4.
y = e^x, y = x, x = 0, x = 1.
Solution:

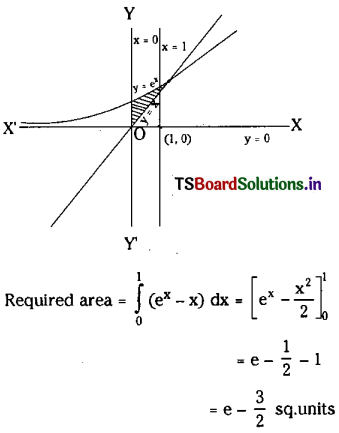
Question 5.
y = sin x, y = cos x, x = 0, x = \(\frac{\pi}{2}\).
Solution:

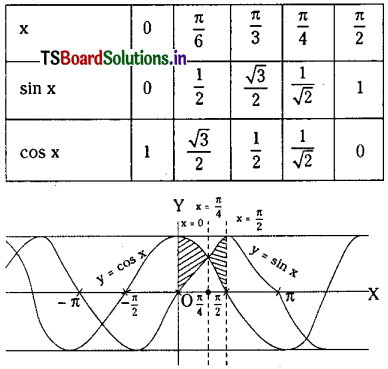
Taking f(x) = sin x and g(x) = cos x
We have sin x – cos x < 0 for x ∈ \(\left[0, \frac{\pi}{4}\right]\) and sin x – cos x > 0 for x ∈ \(\left[\frac{\pi}{4}, \frac{\pi}{2}\right]\)
Area enclosed between y = sin x, y = cos x, x = 0, x = \(\frac{\pi}{2}\) is

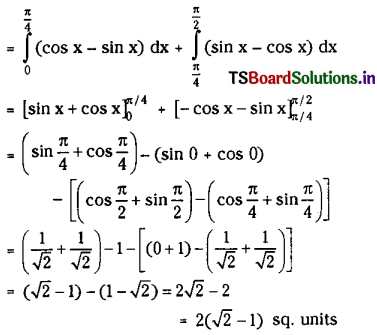
Question 6.
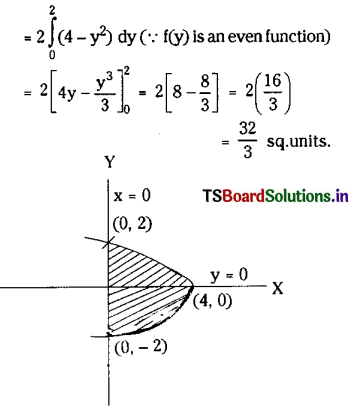
x = 4 – y², x = 0.
Solution:
The curve x = 4 – y² cuts Y – axis at x = 0.
Hence 4 – y² = 0
⇒ y = ± 2
∴ Points of intersection are given by (0, 2) and (0, – 2).
∴ Area subtended by Y-axis, the curve x = 4 – y² is given by \(A=\int_{-2}^2 x d y=\int_{-2}^2\left(4-y^2\right) d y\)

Question 7.
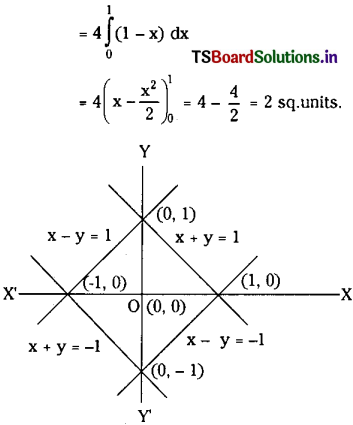
Find the area enclosed with in the curve |x| + |y| = 1.
Solution:
The given equation of the curve is |x| + |y| = 1 which represents ± x ± y = 1 representing four different lines forming a square.
Consider the line x + y = 1
⇒ y = 1 – x
If the line touches the X-axis then y = 0 and one of the points of intersection with X-axis is (1, 0).
Since the curve is symmetric with respect to coordinate axes, area bounded by |x| + |y| = 1 is

II.

Question 1.
x = 2 – 5y – 3y², x = 0.
Solution:
Solving x = 2 – 5y – 3y² and x = 0
We get – 3y² – 5y + 2 = 0
⇒ 3y² + 5y – 2 = 0
⇒ 3y² + 6y – y – 2 = 0
⇒ 3y (y + 2) – 1 (y + 2) = 0
⇒ (y + 2)(3y – 1) = 0
⇒ y = -2 or y = \(\frac{1}{3}\)
Required area subtended by the curve x = 2 – 5y – 3y², Y-axis and y = \(\frac{1}{3}\) and y = – 2 is

Question 2.
x² = 4y, x = 2, y = 0.
Solution:

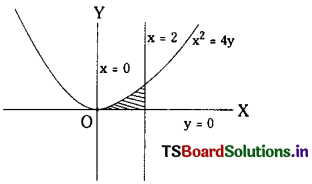
The given equation x² = 4y represents parabola which is symmetric with respect to Y-axis.
When x = 2 we have
4y = 4
⇒ y = 1
Hence P(2, 1) is the point of intersection.
∴ Area bounded by x² = 4y, and x = 0, x = 2 is
A = \(\int_0^2 y d x=\int_0^2 \frac{x^2}{4} d x\)
= \(\frac{1}{4}\left[\frac{x^3}{3}\right]_0^2=\frac{1}{4}\left(\frac{8}{3}\right)=\frac{2}{3}\) sq. units.

Question 3.
y² = 3x, x = 3.
Solution:
y² = 3x is a parabola which is symmetrical to X-axis;
when x = 3 then y² = 9
⇒ y = ± 3
Hence (3, 3) and (3, – 3) are the points of intersection.

Question 4.
y = x², y = 2x
Solution:

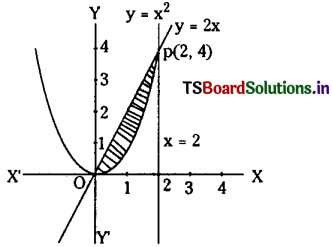
Given y = x² and y = 2x
solving these we get x² – 2x = 0
⇒ x (x – 2) = 0
⇒ x = 0 or x = 2
∴ y = 0 or y = 4
Hence O(0, 0) and P(2, 4) are the points of intersection of (1) and (2).
∴ Required area bounded by y = x² and y = 2x is
= \(\int_0^2\left(2 x-x^2\right) d x=2\left[\frac{x^2}{2}\right]_0^2-\left[\frac{x^3}{3}\right]_0^2\)
= \(2\left[\frac{4}{2}\right]-\left[\frac{8}{3}\right]\)
= 4 – \(\frac{8}{3}\) = \(\frac{4}{3}\) sq. units.

Question 5.
y = sin 2x, y = √3 sin x, x = 0 and x = \(\frac{\pi}{6}\).
Solution:

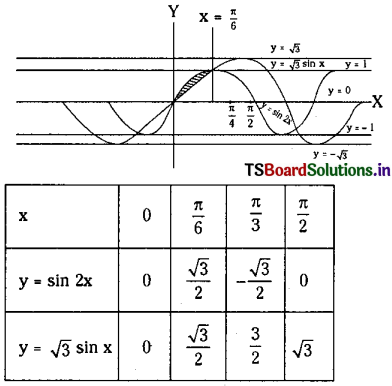
Given curves are y = sin 2x …….(1)
and y = √3 sin x ……..(2)
When x = \(\frac{\pi}{6}\) then y = \(\frac{\sqrt{3}}{2}\)
∴ \(\left(\frac{\pi}{6}, \frac{\sqrt{3}}{2}\right)\) is a point of intersection (1) and (2).
∴ Area enclosed between the curves

Question 6.
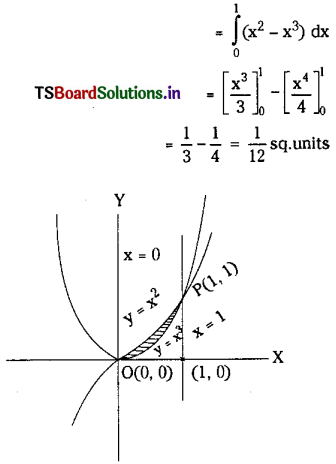
y = x², y = x³.
Solution:
Given curves are y = x² and y = x³
By solving we get x² = x³
⇒ x² (x – 1) = 0
⇒ x = 0 or x = 1
∴ y = 0 or y = 1
Hence (0, 0) and (1, 1) are the points of intersection.
Also f(x) = x² and g(x) = x³ and f(x) > g(x) in [0, 1].
∴ Area bounded by the curves

Question 7.
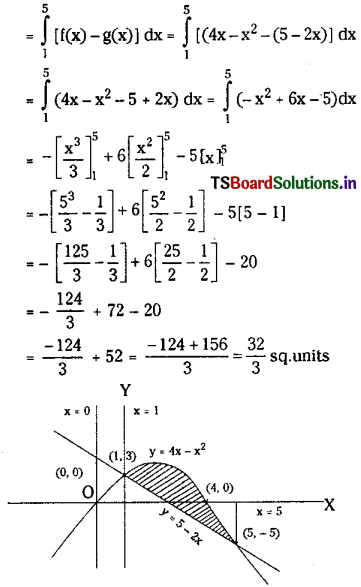
y = 4x – x², y = 5 – 2x.
Solution:
The given equations of curves are denoted by
y = f(x) = 4x – x² ……(1)
y = g(x) = 5 – 2x ……..(2)
Solving (1) and (2)
4x – x² = 5 – 2x
⇒ x² – 2x – 4x + 5 = 0
⇒ x² – 6x + 5 = 0
⇒ (x – 5) (x – 1) = 0
⇒ x = 1 or 5
When x = 1, y = 3 and x = 5, y = -5
Hence P(1, 3) and Q(5, – 5) are the two points of intersection.
Now f(x) > g(x) in [1, 5].
∴ Area bounded between the curves is

Question 8.
Find the area in sq.units bounded by the X-axis, part of the curve y = 1 + \(\frac{8}{x^2}\) and the ordinates x = 2 and x = 4.
Solution:
In [2, 4] we have the equation of the curve given by y = 1 + \(\frac{8}{x^2}\)
∴ Area bounded by the curve y = 1 + \(\frac{8}{x^2}\)
X-axis and the ordinates x = 2 and x = 4 is

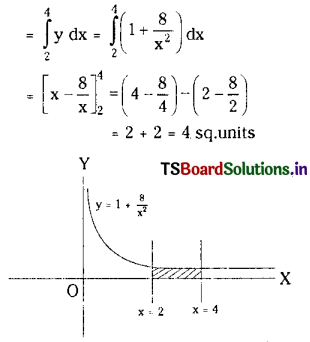
Question 9.
Find the area of the region bounded by the parabolas y2 = 4x and x2 = 4y.
Solution:
Given equations of curves are
y² = 4x ……..(1)
x² = 4y ……..(2)
Solving (1) and (2) the points of intersection can be obtained.
y² = 4x
⇒ y⁴ = 16x²
⇒ y⁴ = 64y
⇒ y = 4
∴ 4x = y²
⇒ 4x = 16
⇒ x = 4
Points of intersection are (0, 0) and (4, 4).

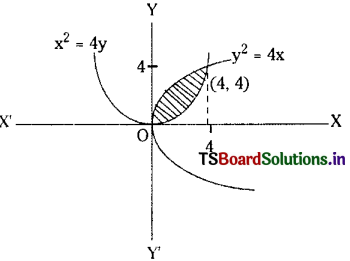
∴ Area bounded between the parabolas

Question 10.
Find the area bounded by the curve y = log x, the X-axis and the straight line x = e.
Solution:
Area bounded by the curve y = \(\log _e x\), X-axis
and the straight line x = e is \(\int_1^e \log _e x d x\)
= \([\mathrm{x} \log \mathrm{x}]_{\mathrm{1}}^{\mathrm{e}}-\int_1^{\mathrm{e}} \mathrm{dx}\) (∵ when x = e, y = loge e = 1)
= (e – 0) – (e – 1)
= 1 sq.units

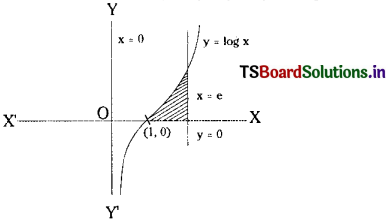
III.

Question 1.
y = x² + 1, y = 2x – 2, x = -1, x = 2.
Solution:
Equations of given curves are
y = x² + 1 ……..(1)
y = 2x – 2 ………(2)

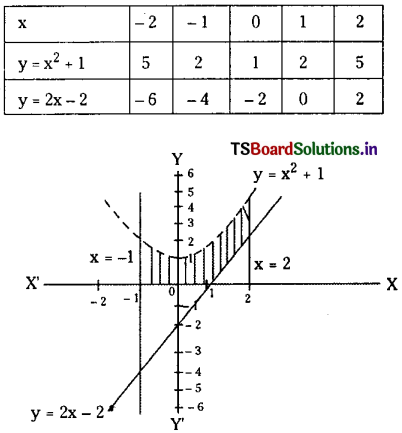
Take f(x) = x² + 1 and g(x) = 2x – 1
we find f(x) > g(x) ∀ x ∈ [- 1, 2]
Hence area bounded by y = x² + 1 and y = 2x – 2 is

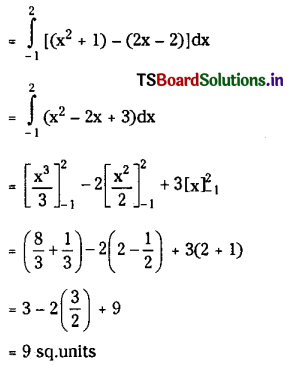
Question 2.
y² = 4x, y² = 4(4 – x).
Solution:
Equations of the curves are
y² = 4x ………(1)
y² = 4(4 – x) ………(2)
From (1) and (2)
4x = 4(4 – x)
⇒ 8x = 16
⇒ x = 2
∴ y² = 8
⇒ y = ± 2√2
∴ The points of intersection are (2, 2√2), (2, – 2√2)

Question 3.
y = 2 – x², y = x².
Solution:
The given curves are
y = 2 – x² ………(1)
y = x² …….(2)

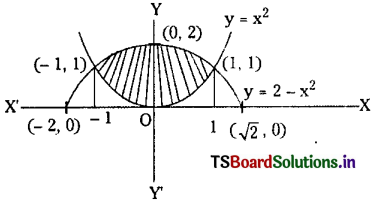
Solving (1) and (2) we get
2 – x² = x²
⇒ 2x² = 2
⇒ x² = 1
⇒ x = ± 1
∴ y = 1
Hence points of intersection of curves are (1, 1), (- 1, 1)
∴ Area bounded between the curves

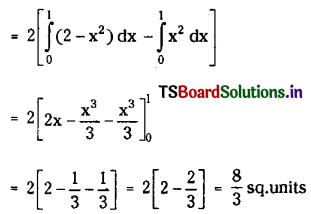
Question 4.
Show that the area enclosed between the curves y² = 12 (x + 3) and y² = 20 (5 – x) is 64 \(\sqrt{\frac{5}{3}}\).
Solution:

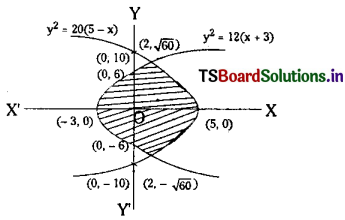
Given curves are y² = 12 (x + 3) …….(1)
and y² = 20 (5 – x) ………(2)
Solving (1) and (2) we get
12 (x + 3) = 20 (5 – x)
⇒ 12x + 36 = 100 – 20x
⇒ 32x = 64
⇒ x = 2
∴ y² = 20(5 – 2) = 60
⇒ y = ± 2√15
∴ Points of intersection are B(2, 2√15) and B'(2, – 2√5).
The given equations represent these parabolas
(y – β)² = 4a(x – α) and
(y – β)² = – 4a(x – α)
∴ Vertex of (1) is A(- 3, 0) and vertex of (2) is A'(5, 0).
∴ The required area is symmetrical about X-axis.
∴ Area bounded by curves is ABA’B’

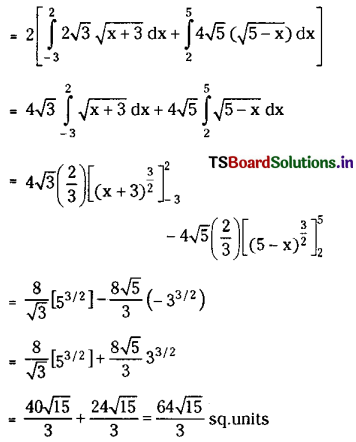
Question 5.
Find the area of the region {(x, y): x² – x – 1 ≤ y ≤ -1}.
Solution:
Consider y = x² – x – 1 ……(1)
and y = – 1 ……(2)

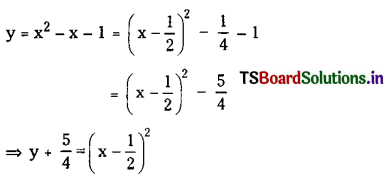
Which represents a parabola in the form (x – h)² = 4a(y – k) where vertex \(\left(\frac{1}{2}, \frac{-5}{4}\right)\) with 4a = 1.
Also x² – x – 1 = -1
⇒ x² – x = 0
⇒ x (x – 1) = 0
⇒ x = 0 or 1
∴ Area subtended by the region {(x, y) : x² – x – 1 ≤ y ≤ -1}

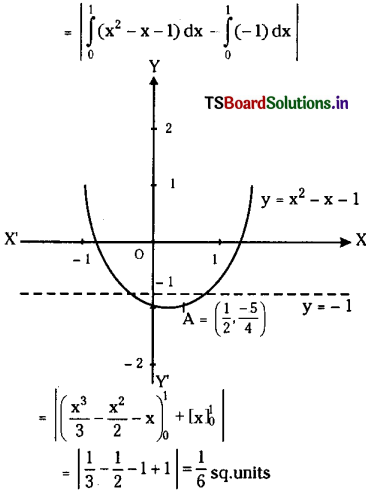
∴ Area of the region {(x, y); x² – x – 1 ≤ y ≤ – 1} is \(\frac{1}{6}\).

Question 6.
The circle x² + y² = 8 is divided into two parts by the parabola 2y = x². Find the area of both the points.
Solution:

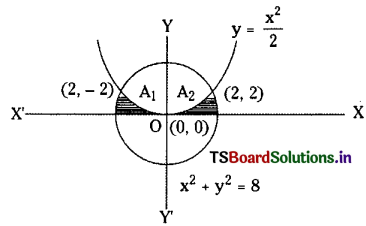
Given curves are x² + y² = 8 ……(1)
and 2y = x² …….(2)
Solving (1) and (2)
x² + \(\frac{x^4}{4}\) = 8
⇒ x⁴ + 4x² – 32 = 0
⇒ x⁴ + 8x² – 4x² – 32 = 0
⇒ x² (x² + 8) – 4(x² + 8) = 0
⇒ (x² – 4) (x² + 8) = 0
⇒ x = ±2 (∵ x² + 8 = 0 is not admissible)
∴ y = 2
Hence the points of intersection of (1) and (2) are (2, 2) (- 2, 2).
Let the area bounded between (1) and (2) be sum of two areas A₁ and A₂ as shown in the figure. Then

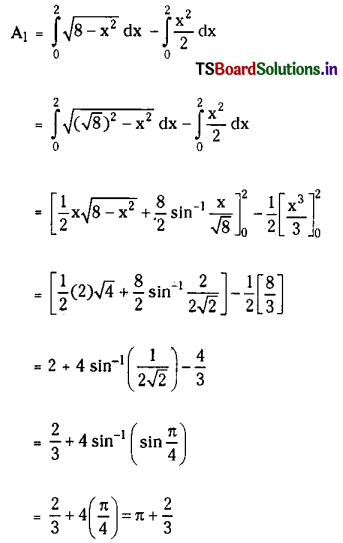
Again
A₂ = π + \(\frac{2}{3}\) (Since the bounded position is symmetric)
∴ Area bounded by the curves = 2π + \(\frac{4}{3}\) sq.units
Area bounded by the circle = πr² = 8π when r = 2√2
∴ Area of the remaining portion = 8π – (2π + \(\frac{4}{3}\)) = 6π – \(\frac{4}{3}\) sq.units.

Question 7.
Show that the area of the region bounded by \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 (ellipse) is πab. Also deduce the area of the circle x² + y² = a². (June ’10)
Solution:

Given equation of ellipse is \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1
Since the ellipse is symmetric with respect to coordinate axes we have

∴ Area of the region bounded by \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 is πab sq.units
Substituting b = a in the above result we have the area of circle given by πa(a) = πa² sq.units

Question 8.
Find the area of the region enclosed by the curves y = sin πx, y = x² – x, x = 2.
Solution:
The graphs of the given equations y = sin πx and y = x² – x, x = 2 are shown below.

Question 9.
Let AOB be the positive quadrant of the ellipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}\) = 1 with OA = a, OB = b. Then show that the area bounded between the chord AB and the arc AB of the ellipse is \(\frac{(\pi-2) a b}{4}\).
Solution:

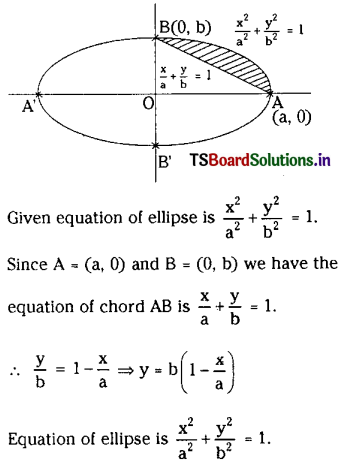
Question 10.
Prove that the curves y² = 4x and x² = 4y divide the area of square bounded by the lines x = 0, x = 4, y = 4 and y = 0 into three equal parts.
Solution:

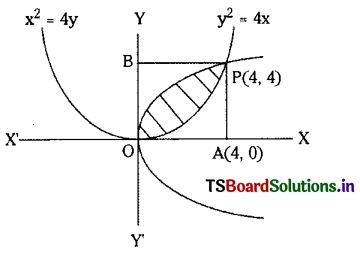
The given curves are y² = 4x ……(1) and x² = 4y ………(2)
Solving y⁴ = 16x² = 64y
⇒ y(y³ – 64) = o
⇒ y = 0 or y = 4
When y = 4 we have 4x = 16 ⇒ x = 4
∴ Points of intersection of parabolas is P(4, 4).
∴ Area bounded by the parabolas

Area of the square formed = (OA)² = (4)² = 16
Since the area bounded by the parabolas x² = 4y and y² = 4x is \(\frac{1}{2}\) sq.units.
Which is one third of the area of square we conclude that the curves y² = 4x and x² = 4y divide the area of the square bounded by x = 0, x = 4, y = 0, y = 4 into three equal parts.