TS Inter 2nd Year Maths 2A Solutions Chapter 4 Theory of Equations Ex 4(c)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 4 Theory of Equations Ex 4(c) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 4 Theory of Equations Ex 4(c)

I.
Question 1.
From the polynomial equation, whose roots are
i) 2 + 3i, 2 – 3i, 1 + i, 1 – i
ii) 3, 2, 1 + i, 1 – i
iii) 1 + i, 1 – i, – 1 + i, – 1 – i
iv) 1 + i, 1 – i, 1 + i, 1 – i
Solution:
i) Given roots are 2 + 3i, 2 – 3i, 1 + i, 1 – i.
∴ The equation with given roots is (x – (2 + 3i)) (x – (2 – 3i)) (x – (1 + i)) (x – (1 – i)) = 0
⇒ (x² – 4x + 13) (x² – 2x + 2) = 0
⇒ x⁴ – 6x³ + 23x² – 34x + 26 = 0
Required equation is x⁴ – 6x³ + 23x² – 34x + 26 = 0.

ii) Given roots are 3, 2, 1 + i, 1 – i.
∴ The required equation is (x – 3) (x – 2) (x – (1 + i)) (x – (1 – i)) = 0
⇒ (x² – 5x + 6) (x² – 2x + 2) = 0
⇒ x⁴ – 7x³ + 18x² – 22x + 12 = 0.

iii) Given roots are 1 + i, 1 – i, – 1 + i, – 1 – i
∴ The required equation is (x – (1 + i)) (x – (1 – i)) (x – (- 1 + i)) (x – (- 1 – 0) = 0
⇒ (x² – 2x + 2) (x² + 2x + 2) = 0
⇒ x⁴ + 4 = 0.

iv) Given roots are 1 + i, 1 – i, 1 + i, 1 – i
∴ The required equation is (x – (1 + i)) (x – (1 – i)) (x – (1 + i)) (x – (1 – i)) = 0
⇒ (x – (1 + i))² (x – (1 – i))² = 0
⇒ (x² – 2x + 2)² = 0
⇒ x⁴ – 4x³ + 8x² – 8x + 4 = 0.

Question 2.
Form the polynomial equation with ratio¬nal coefficients whose roots are
i) 4√3, 5 + 2i
ii) 1 + 5i, 5 – i
iii) i – √5
iv) – √3 + i√2
Solution:
i) Given 4√3, 5 + 2i are the two roots of polynomial equation with rational coeffi-cients.
For the polynomial equation, with ratio-nal coefficients, the roots are conjugate surds and conjugate complex numbers.
Hence (i) If 4√3 is a root, then – 4√3 is also a root.
(ii) If 5 + 2i is a root, then 5 – 2i is also a root.
∴ The roots are 4√3 , – 4√3, 5 + 2i, 5 – 2i.
∴ The required equation with given roots is (x – 4√3 ) (x + 4√3 ) (x – (5 + 2i)) (x – (5 – 2i)) = 0
⇒ (x² – 48) (x² – 10x + 29) = 0
⇒ x⁴ – 10x³ + 29x² – 48x² + 480x – 1932 = 0
⇒ x⁴ – 10x³ – 19x² + 480x – 1932 = 0.

ii) Given 1 + 5i, 5 – i are the roots of polyno-mial equation with rational coefficients. For the polynomial equation with rational coefficients, the roots are conjugate surds and conjugate complex numbers.
∴ (i) if 1 + 5i is a root, then 1 – 5i is also a root.
(ii) If 5 – i is a root, then 5 + i is also a root.
∴ The roots are 1 + 5i, 1 – 5i, 5 – i, 5 + i
∴ The required equation is
(x – (1 + 5i)) (x – (1 – 5i)) (x – (5 – i)) (x – (5 + i)) = 0
⇒ (x² – 2x + 26) (x² – 10x + 26) = 0
⇒ x⁴ – 12x³ + 72x² – 312x + 676 = 0.

iii) Given i – √5 is a root of polynomial equation with rational coefficients.
If i – √5 is a root, then i + √5 , – i – √5 and – i + √5 are also roots.
∴. The roots are i – √5, – i – √5, i + √5, – i + √5
∴ The required equation is (x – (i – √5)) (x – (- i – √5))
(x – (i + √5)) (x – (i +√5)) = 0
⇒ (x² + 2√5x + 6) (x² – 2√5x + 6) = 0
⇒ x⁴ – 8x² + 36 = 0.

iv)Given – √3 + i√2 is a root of polynomial equation with rational coefficients.
∴If – √3 + i√2 is a root then – √3 – i√2, √3 + i√2, √3 – i √2 are also roots.
The roots are – √3 + i√2, – √3 – i√2, √3 + i√2, √3 – i √2
∴ The required equation is (x – (- √3 + i√2)) (x – (- √3 – i√2))
(x – (√3 + i√2)) (x – (√3 – i √2)) = 0
⇒ (x² + 2√3x + 5) (x² – 2√3x +5) = o
⇒ x⁴ – 12x² + 25 = 0.

II.
Question 1.
Solve the equation x4 + 2×3 – 5×2 + 6x + 2 = 0 given that I + ¡ is one of its roots.
Solution:
Given equation is
x⁴ + 2x³ – 5x² + 6x + 2 = 0 ……………(1)
Let f(x) = x⁴ + 2x³ – 5x² + 6x + 2
Given 1 + i is a root.
1 – i s also root. (∵ coefficients of (1) are rational)
∴ (x – (1 + i)) (x – (1 – i)) is a factorof f(x).
= (x² – 2x + 2) is a factor of f(x).
By synthetic division,

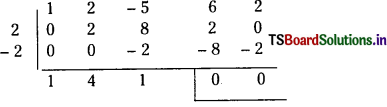
∴ f(x) = (x² – 2x 2) (x² + 4x + 1).
∴ Equation (1)
⇒ (x² – 2x + 2) (x² + 4x + 1) = 0
∴ x² – 2x + 2 = 0 or x² + 4x + 1 = 0
∴ x = 1 ± i; x = – 2 ± √3
∴ The roots of given equation are 1 ± i. – 2 ± √3.

Question 2.
Solve the equation 3x³ – 4x² + x + 88 = 0 which has 2 – \(\sqrt{-7}\) as a root.
Solution:
Given equation is 3x³ – 4x² + x + 88 = 0 ……………(1)
Given 2 – \(\sqrt{-7}\) is a root.
2 + \(\sqrt{-7}\) is also a root
(∵ coefficients of (I) are rational)
Let f(x) = 3x³ – 4x² + x + 88
∴ (x – (2 – \(\sqrt{-7}\))) (x – (2 + \(\sqrt{-7}\))) a factor of f(x).
(x² – 4x 11) is a factor of f(x).
We divide f(x) by x² – 4x + 11
∴ By synthetic division,

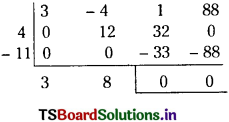
∴ f(x) = (x² – 4x +11) (3x + 8)
∴ Equation (1)
(x² – 4x + 11) (3x + 8) = 0
x² – 4x + 11 = 0 or 3x + 8 = 0
x = 2 ± \(\sqrt{-7}\) or x = \(\frac{-8}{3}\)
The roots of given equation are 2 ± \(\sqrt{-7}\), \(\frac{-8}{3}\).

Question 3.
Solve x⁴ – 4x² + 8x + 35 = 0, given that 2 + i√3 is a root.
Solution:
Given equation is x⁴ – 4x² + 8x + 35 = 0 …………(1)
Let 1(x) = x⁴ – 4x² + 8x + 35
Given 2 + i√3 is a root of (1).
⇒ 2 – √3 if is also a root.
(∵ coefficients 0f (1) are rational)
∴ (x – (2 + i√3)) (x – (2 – i√3)) is a factor of f(x).
⇒ (x² – 4x + 7) is a factor of f(x).
We divide f(x) by x² – 4x + 7.
By synthetic division,

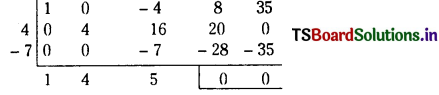
∴ f(x) = (x² – 4x + 7) (x² + 4x + 5)
∴ Equation (1)
⇒ (x² – 4x 7) (x²2 + 4x + 5) = 0
⇒ x² – 4x + 7 = 0 (or) x² + 4x + 5 = 0
⇒ x = – 2 ± i
∴ The roots of given equation are 2 ± √3, – 2 ± i.

Question 4.
Solve the equation x⁴ – 6x³ + 11x² – 10x + 2 = 0, given that 2 + √3 is a root of the equation.
Solution:
Given equation is
x⁴ – 6x³ + 11x² – 10x + 2 = 0 …………..(1)
Let f(x) =x⁴ – 6x³ + 11x² – 10x + 2
given 2 + √3 is a root of (1)
⇒ 2 – √3 is also a root of (1)
(∵ coefficients of (1) are rational)
∴ (x – (2 + √3)) (x – (2 – √3) is a factor of f(x).
⇒ (x² – 4x + 1) is a factor of f(x).
We divide f(x) by x² – 4x + 1.
By synthetic division,

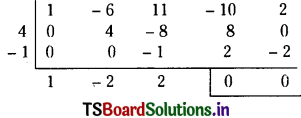
∴ f(x) = (x² – 4x + 1) (x² – 2x + 2)
∴ Equation (1)
⇒ (x² – 4x + 1) (x² – 2x + 2) = 0
⇒ x² – 4x + 1 = 0 (or) x² – 2x + 2 = 0
⇒ x = 2 ± √3 (or) x = 1 ± i
∴ The roots of given equation are 2 ± √3, 1 ± i.

Question 5.
Given that – 2 + \(\sqrt{-7}\) is a root of the equation x⁴ + 2x² – 16x + 77 = 0, solve it completely.
Solution:
Given equation is x⁴ + 2x² – 16x + 77 = 0 …………….(1)
Let f(x) = x⁴ + 2x² – 16x + 77
Given – 2 + \(\sqrt{-7}\) is a root of (1)
⇒ – 2 –\(\sqrt{-7}\) is also a root of (1)
(∵ coefficients of (1) are rational)
∴ (x – (- 2 + \(\sqrt{-7}\))) (x -(- 2 – \(\sqrt{-7}\))) is a factor of f(x).
⇒ (x² + 4x + 11) is a factor of f(x).
We divide f(x) by x² + 4x + 11.
∴ By synthetic division,

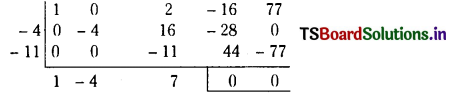
Equation (1)
⇒ (x² – 4x + 11) (x² – 4x + 7) = 0
∴ x² + 4x + 11 = 0 or x² – 4x + 7 = 0
∴ x = -2 ± ypf ; x = 2 ± h/3
∴ The roots are – 2 ± \(\sqrt{-7}\), 2 ± i√3 .

Question 6.
Solve the equation x⁴ + 2x³ – 16x² – 22x + 7 = 0, given that 2 – √3 is one of its roots.
Solution:
Given equation is x⁴ + 2x³ – 16x² – 22x + 7 = 0 …………..(1)
Let f(x) = x⁴ + 2x³ – 16x² – 22x + 7
Given 2 – √3 is a root of (1)
⇒ 2 + √3 is also a root of (1). ;
(∵ coefficients of (1) are rational)
(x – (2 – √3) (x – (2 + √3)) is a factor of f(x).
∵ (x² – 4x + 1) is a factor of f(x).
We divide f(x) by x² – 4x + 1.
By synthetic division,

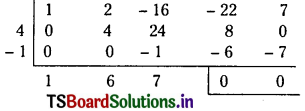
f(x) = (x² – 4x + 1) (x² + 6x + 7)
Equation (1)
∵ (x² – 4x + 1) (x² + 6x + 7) = 0
∵ x² – 4x + 1 = 0 or x² + 6x + 7 = 0
∵ x = 2 ± √3 x = – 3 ± √2
The roots of given equation are 2 ± √3, – 3 ± √2.

Question 7.
Solve the equation 3x⁵ – 4x⁴ – 42x³ + 56x² + 27x – 36 = 0, given that √2 + √5 is one of its roots.
Solution:
Given equation is
3x⁵ – 4x⁴ – 42x³ + 56x² + 27x – 36 = 0 …………….(1)
Given √2 + √5 is a root of (1)
⇒ √2 – √5, – √2 – √5, – √2 + √5 are also roots of (1).
Let α be the 5th root of (1)
Sum of the roots = \(\frac{4}{3}\)
∴ α + √2 + √5 + √2 – √5 – √2 – √5 – √2 + √5 = \(\frac{4}{3}\)
α = \(\frac{4}{3}\)
∴ The roots are \(\frac{4}{3}\), √2 + √5, √2 – √5, – √2 + √5, – √2 – √5.

Question 8.
Solve the equation x⁴ – 9x³ + 27x² – 29x + 6 = 0, given that one root is 2 – √3.
Solution:
Given equation is x⁴ – 9x³ + 27x² – 29x + 6 = 0 …………..(1)
Let f(x) = x⁴ – 9x³ + 27x² – 29x + 6
Given 2 – √3 is a root of (1)
∴ 2 + √3 is also root of (1).
(∵ coefficients of (1) are rational)
∴ (x – (2 – √3)) (x – (2 + √3)) is a factor of f(x).
⇒ (x² – 4x + 1) is a factor of f(x).
We divide f(x) by (x² – 4x + 1).
By synthetic division,

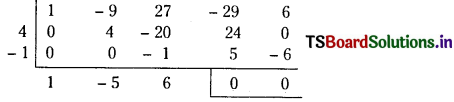
f(x) = (x² – 4x + 1) (x² – 5x + 6)
∴ Equation (1)
⇒ (x² – 4x + 1) (x² – 5x + 6) = 0
⇒ x² – 4x + 1 = 0 or x² – 5x + 6 = 0
⇒ x = 2 ± √3 or x = 2 or x = 3
∴ The roots are 2 ± √3 , 2, 3.

Question 9.
Show that the equation \(\frac{a^2}{x-a^{\prime}}+\frac{b^2}{x-b^{\prime}}+\frac{c^2}{x-c^{\prime}}+\ldots+\frac{k^2}{x-k^{\prime}}\) = x – m. where a, b, c ………….., k m, a, b, ……………., k are all real numbers can not have a non – real roots.
Solution:
Given that is
\(\frac{a^2}{x-a^{\prime}}+\frac{b^2}{x-b^{\prime}}+\frac{c^2}{x-c^{\prime}}+\ldots+\frac{k^2}{x-k^{\prime}}\) = x – m
⇒ \(\frac{a^2}{x-a^{\prime}}+\frac{b^2}{x-b^{\prime}}+\frac{c^2}{x-c^{\prime}}+\ldots+\frac{\mathrm{k}^2}{\mathrm{x}-\mathrm{k}^{\prime}}\) – x + m = 0 ………….(1)
Let us assume p + iq is a root of (1)

This is a contradiction since none of the factors of the left side of the above equation is zero.
Hence all the roots of given equation are real.