TS Inter 2nd Year Maths 2A Solutions Chapter 4 Theory of Equations Ex 4(b)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 4 Theory of Equations Ex 4(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 4 Theory of Equations Ex 4(b)

I.
Question 1.
Solve x³ – 3x² – 16x + 48 = 0, given that the sum of two roots is zero.
Solution:
Let α, β, γ be the roots of
x³ – 3x² – 16x + 48 = 0 ………….(1)
Given that the sum of two roots is zero.
Let α + β = 0 …………(2)
But from (1) we have α + β + γ = 3
⇒ γ = 3
Hence αβγ = – 48
⇒ αβ = – 16
We know that,
(α + β)² – (α – β)² = 4αβ
⇒ (α – β)² = 64
⇒ α – β = ± 8.

i) When α – β = 8
⇒ 2α = 8 (∵ from (2))
⇒ α = 4
∴ β = – 4.

ii) When α – β = – 8
⇒ 2α = – 8 (∵ from (2))
⇒ α = – 4
∴ β = 4.
The roots of given equation are 4, – 4 and 3.

Question 2.
Find the condition that x³ – px² + qx – r = 0 may have the sum of two of its roots zero.
Solution:
Given equation is x³ – px² + qx – r = 0
Let α, β, γ be the roots.
∴ α + β + γ = p …………..(1)
Given sum of two of its roots is zero.
∴ (1) ⇒ α + 0 = p
i. e„ α = p
Substituting in given equation, we get p³ – p³ + pq – r = 0
⇒ pq – r = 0
⇒ Pq = r.

Question 3.
Given that the roots of x³ + 3px² + 3qx + r = 0 are in
i) A.P., show that 2p³ – 3qp + r = 0
ii) G.P., show that p³r = q³
iii) H.P., show that 2q³ = r (3pq – r).
Solution:
Given cubic equation is
x³ + 3px² + 3qx + r = 0 ……………..(1)
Let α, β, γ be its roots.

i) When the roots are in A.P. :
i.e., 2β = α + γ
from (1) α + β + γ = – 3p
⇒ (α + γ) + P = – 3p
⇒ 2β + β = – 3p
⇒ 3β = – 3p
⇒ β = – P
Substituting in given equation, we get
– p³ + 3p³ – 3pq + r = 0
⇒ 2p³ – 3pq + r = 0.

ii) When the roots are in G.P. :
∴ β² = αγ
from (1) αβγ = – r
⇒ β³ = – r
⇒ β = – r^1/3
Substituting in (1), we get
(- r^1/3)³ + 3pr^2/3 – 3qr^1/3 + r = 0
⇒ 3pr^2/3 = 3qr^1/3
⇒ P³r = q³.

iii) When the roots are in H.P. :
β = \(\frac{2 \alpha \gamma}{\alpha+\gamma}\)
⇒ β² = \(\frac{2 \alpha \beta \gamma}{(\alpha+\beta+\gamma)-\beta}\)
⇒ β² = \(\frac{-2 r}{-3 p-\beta}\)
⇒ β² + 3pβ² = 2r (∵ β is a root of (1))
⇒ – 3qβ – r = 2r
β = – \(\frac{r}{q}\)
Substituting in (1) we get
\(\frac{-r^3}{q^3}+\frac{3 p r^2}{q^2}-\frac{3 q r}{q}\) + r = 0
⇒ 2q³ = r(3pq – r).

Question 4.
Find the condition that x³ – px² + qx – r = 0 may have the roots in G.P.
Solution:
Let α, β, γ be the roots of
x³ – px² + qx – r = 0
If α, β, γ are in G.P., then
β² = αγ
(1) ⇒ αβγ = r
⇒ β³ = r
β = r^1/3
Substituting in (1), we get
(r^1/3)³ – p(r^1/3)² + q(r^1/3) – r = 0
⇒ pr^2/3 = qr^1/3
⇒ p³r² = q³r
⇒ q³ = p³r.

II.
Question 1.
Solve 9x³ – 15x² 7x – 1 = 0, given that two of its roots are equal.
Solution:
Given cubic equation is
9x³ – 15x² – 7x – 1 = 0 ……………. (1)
Suppose α, β, γ are the roots of (1)
∴ α + β + γ = \(\frac{15}{9}=\frac{5}{3}\)
αβ + βγ + γα = \(\frac{7}{9}\)
αβγ = \(\frac{1}{9}\)
According to the problem, α = β (∵ two of its roots are equal)
∴ 2α + γ = \(\frac{5}{3}\)
⇒ γ = \(\frac{5}{3}\) – 2α
Also, α² + 2αγ = \(\frac{7}{9}\)
⇒ α² + 2α (\(\frac{5}{3}\) – 2α) = \(\frac{7}{9}\)
⇒ 27α² – 30α + 7 = 0
⇒ (3α – 1) (9α – 7) = 0
∴ α = \(\frac{1}{3}\) or α = \(\frac{7}{9}\)

Case (i) :
when α = \(\frac{1}{3}\)
γ = \(\frac{5}{3}\) – 2α
= \(\frac{5}{3}\) – \(\frac{2}{3}\) = 1
∴ The roots are \(\frac{1}{3}\), \(\frac{1}{3}\), 1.

Case – (ii):
When α = \(\frac{7}{9}\)
γ = \(\frac{5}{3}\) – 2α
= \(\frac{5}{3}-\frac{14}{9}\) = \(\frac{1}{9}\)
Which is impossible as
αβγ = \(\frac{7}{9} \cdot \frac{7}{9} \cdot \frac{1}{9}\) ≠ \(\frac{1}{9}\)
∴ The roots are \(\frac{1}{3}\), \(\frac{1}{3}\), 1.

Question 2.
Given that one root of 2x³ + 3x² – 8x + 3 = 0 is double the other root, find the roots of equation.
Solution:
Given cubic equation is
2x³ + 3x² – 8x + 3= 0 ……………..(1)
Suppose α, β, γ are the roots of (1).
∴ α + β + γ = \(\frac{-3}{2}\)
αβ + βγ + γα = \(\frac{-8}{2}\) = – 4 …………….(2)
αβγ = \(\frac{-3}{2}\)
Given one root is double the other.
3α + γ = \(\frac{-3}{2}\)
⇒ γ = \(\frac{-3}{2}\) – 3α
Also from (2):
2α² – 3α (\(\frac{3}{2}\) + 3α) = – 4
14α² + 9α – 8 = 0
(2α – 1) (7α + 8) = 0
α = \(\frac{1}{2}\) or α = \(\frac{-8}{7}\).

Case (i):
When α = \(\frac{1}{2}\)
β = 2α = 2 (\(\frac{1}{2}\)) = 1
γ = \(\frac{-3}{2}\) – 3α
= \(\frac{-3}{2} \frac{-3}{2}\) = – 3.
∴ α = \(\frac{1}{2}\), β = 1 and γ = – 3
satisfies αβγ = \(\frac{-3}{2}\)
∴ The roots are \(\frac{1}{2}\), 1, – 3.

Case (ii):
When α = \(\frac{-8}{7}\)
β = 2α = \(\frac{-16}{7}\)
γ = \(\frac{-3}{2}\) – 3α
= \(\frac{-3}{2}+\frac{48}{7}=\frac{75}{14}\)
But α = \(\frac{-8}{7}\), β = \(\frac{-16}{7}\) and γ = \(\frac{75}{14}\) do not satisfy αβγ = \(\frac{-3}{2}\).
Hence the roots of given equation are \(\frac{1}{2}\), 1, – 3.

Question 3.
Solve x³ – 9x² + 14x + 24 = 0, given that two of the roots are in the ratio 3 : 2.
Solution:
Given cubic equation is
x³ – 9x² + 14x + 24 = 0 ……….(1)
Let α, β, γ be the roots of (1)
∴ α + β + γ = 9, αβ + βγ + γα = 14, αβγ = – 24 ……………..(2)
Given two roots are in the ratio 3 : 2,
let α : β = 3 : 2
⇒ β = \(\frac{2 \alpha}{3}\)
Now from (2) \(\frac{5 \alpha}{3}\) + γ = 9
⇒ γ = 9 – \(\frac{5 \alpha}{3}\)
Also, \(\frac{2}{3}\) α² + (9 – \(\frac{5 \alpha}{3}\)) \(\frac{5 \alpha}{3}\) = 14
⇒ 2α² + \(\frac{5 \alpha(27-5 \alpha)}{3}\) = 42
⇒ 19α² – 135α + 126 = 0
⇒ (19α – 21) (α – 6) = 0
⇒ α = \(\frac{21}{19}\) or α = 6.

Case (i):
When α = \(\frac{21}{19}\)
β = \(\frac{2}{3}(\alpha)=\frac{2}{3}\left(\frac{21}{19}\right)=\frac{14}{19}\)
γ = \(9-\frac{5 \alpha}{3}=9-\frac{5}{3}\left(\frac{21}{19}\right)=\frac{136}{19}\)
These values do not satisfy αβγ = – 24.

Case – (ii) :
When α = 6
β = \(\frac{2}{3}(\alpha)=\frac{2}{3}(6)\) = 4
γ = \(9-\frac{5 \alpha}{3}=9-\frac{5}{3}(6)\) = – 1
These values satisfy αβγ = – 24.
∴ The roots of given equation are 6, 4, – 1.

Question 4.
Solve the following equations, given that the roots of each are in A.P.
i) 8x³ – 36x² – 18x + 81 = 0
ii) x³ – 3x² – 6x + 8 = 0
Solution:
i) Given cubic equation is
8x³ – 36x² – 18x + 81 = 0 …………….(1)
Given the roots are in A.P.
∴ α – d, α, α + d be the roots.
∴ Sum of the roots 3α = \(\frac{36}{8}\)
⇒ α = \(\frac{3}{2}\)
∴ x – \(\frac{3}{2}\) is a factor of 8x³ – 36x² – 18x + 81
By synthetic division,

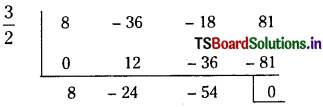
8x³ – 36x² – 18x + 81 = (x – \(\frac{3}{2}\)) (8x² – 24x – 54)
∴ Equation (1)
⇒ (x – \(\frac{3}{2}\)) (8x² – 24x – 54) = 0
⇒ (x – \(\frac{3}{2}\)) (2x + 3) (2x – 9) = 0
⇒ x = – \(\frac{3}{2}\) or x = \(\frac{3}{2}\) or x = \(\frac{9}{2}\)
∴ The roots are \(\frac{-3}{2}\), \(\frac{3}{2}\), \(\frac{3}{2}\).

ii) Given roots of cubic equation
x³ – 3x² – 6x + 8 = 0 ……………(1) are in G.P.
Let α – d, α, α + d be the roots.
∴ Sum of the roots 3α = 3
⇒ α = 1
∴ (x – 1) is a factor of x³ – 3x² – 6x + 8.
By synthetic division,

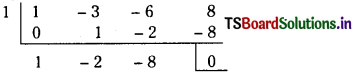
x³ – 3x² – 6x + 8 = (x – 1) (x² – 2x – 8)
∴ Equation (1)
⇒ (x – 1) (x² – 2x – 8) = 0
⇒ (x – 1) (x – 4) (x + 2) = 0
∴ x = 1 or x = 4 or x = – 2.
∴ The roots are – 2, 1, 4.

Question 5.
Solve the following equations, given that the roots of each are in GP.
i) 3x³ – 26x² + 52x – 24= 0
ii) 54x³ – 39x² – 26x + 16 = 0
Solution:
i) Given roots of cubic equation
3x³ – 26x² + 52x – 24 = 0 ……………. (1) are in G.P.
Let \(\frac{\alpha}{r}\), α, αr be the roots.
∴ Product of the roots α³ = \(\frac{24}{3}\) = 8
⇒ α = 2
∴ (x – 2) is a factor of 3x³ – 26x³ + 52x – 24
By synthetic division,

3x³ – 26x² + 52x – 24 = (x – 2) (3x² – 20x + 12)
∴ Equation (1) ⇒ (x – 2) (3x² – 20x + 12) = 0
⇒ (x – 2) (3x – 2) (x – 6) = 0
∴ x = 2 or x = \(\frac{2}{3}\) or x = 6
∴ The roots are \(\frac{2}{3}\), 2, 6.

ii) Given roots of cubic equation.
54x³ – 39x² – 26x + 16 = 0 (1) are in GP.
Let \(\frac{\alpha}{r}\), α, αr be the roots.
∴ Product of the roots α³ = \(\frac{-16}{54}\)
⇒ α³ = \(\frac{-2}{3}\)
∴ (x + \(\frac{2}{3}\)) is a factor 54x³ – 39x² – 26x + 16
By synthetic division,

54x³ – 39x² – 26x + 16 = (x + \(\frac{2}{3}\)) (54x² – 75x + 24)
∴ Equation (1),
(x + \(\frac{2}{3}\)) (54x² – 75x + 24) = 0
(x + \(\frac{2}{3}\)) (18x² – 25x + 8) = 0
(x + \(\frac{2}{3}\)) (9x – 8)(2x – 1) = 0
∴ x = – \(\frac{2}{3}\) or x = \(\frac{8}{9}\) or x = \(\frac{1}{2}\)
∴ The roots are \(\frac{8}{9}\), \(\frac{-2}{3}\), \(\frac{1}{2}\).

Question 6.
Solve the following equations, given that the roots of each are In H.P.
i) 6x³ – 11x² + 6x – 1 = 0
ii) 15x³ – 23x² – 9x – 1 = 0
Solution:
i) Given cubic equation is
6x³ – 11x² + 6x – 1 = 0 …………..(1)
Put y = \(\frac{1}{x}\)
∴ (1) ⇒ \(\frac{6}{y^3}-\frac{11}{y^2}+\frac{6}{y}\) – 1 = 0
⇒ y3 – 6y2 + 11y – 6 = 0 ………… (2)
Given roots of (1) are in H.P.
⇒ Roots of (2) are in AP.
Let a – d, a, a + d be the roots of (2),
∴ Sum of the roots, 3a = 6
⇒ α = 2
∴ (x – 2) is a factor of y³ – 6y² + 11y – 6
By synthetic division

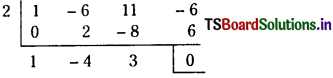
∴ y³ – 6y² + 11y – 6 = (y – 2) (y² – 4y 3)
∴ Equation (2) = (y – 2) (y² – 4y + 3) = 0
⇒ (y – 2) (y – 3) (y – 1) = 0
∴ y = 1 or y = 2 ory = – 3
The roots of (2) are 1, 2, 3.
Hence the roots of (1) are 1, \(\frac{1}{2}\), \(\frac{1}{3}\).

ii) Given cubic equation is
15x³ – 23x² + 9x – 1 = 0 …………….(1)
put y = \(\frac{1}{x}\)
∴ (1) ⇒ y³ – 9y + 23y² – 15 = 0 ………..(2)
Given roots of (1) are in 1-LP.
⇒ Roots of (2) are in A.P.
Let a – d, a, a + d be the roots of (2),
∴ Sum of the roots, 3α = 9
⇒ α = 3
∴ (y – 3) is a factor of y³ – 9y + 23y² – 15.
By synthetic division,

∴ y³ – 9y + 23y² – 15 = (y – 3) (y² – 6y + 5)
∴ Equation (2) = (y – 3) (y2 – 6y + 5) = 0
⇒ (y – 3) (y – 1) (y – 5) = 0
∴ y = 1 or y = 3 or y = 5
∴ The roots of (2) are 1, 3, 5.
Hence the roots of (2) are 1, \(\frac{1}{3}\), \(\frac{1}{5}\).

Question 7.
Solve the following equations, given that they have multiple roots.
i) x⁴ – 6x³ + 13x² – 24x + 36 = 0
ii) 3x⁴ + 16x³ + 24x² – 16 = 0
Solution:
i) Given equation,
x⁴ – 6x³ + 13x² – 24x + 36 = 0 …………..(1)
Let f(x) = x⁴ – 6x³ + 13x² – 24x + 36
f’(x) = 4x³ – 18x² + 26x – 24
= 2 (2x³ – 9x² + 13x – 12)
f’(3) = 2(54 – 81 + 39 – 12)
⇒ f'(3) = o
Now
f(3) = 81 – 162 + 117 – 72 + 36
= f(3) = 0
∴ (x – 3) is a factor of f(x) and f’(x).
∴ 3 is the repeated root of f(x) = 0.
Now we divide f(x) by (x – 3) by using synthetic division.

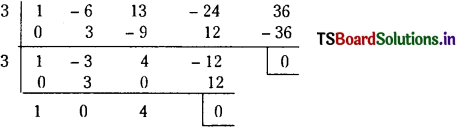
∴ f(x) = (x – 3) (x – 3) (x2 + 4)
∴ Equation (1)
⇒ f(x) = 0
⇒ (x – 3) (x – 3) (x² + 4) = 0
∴ x = 3 or x² + 4 = 0
⇒ x = ±2i
∴ The roots of given equation are 3, 3, ± 2i.

ii) Given equation is
3x⁴ + 16x³ + 24x² – 16 = 0 …………..(1)
Let f(x) = 3x⁴ + 16x³+ 24x² – 16
⇒ f'(x) = 12x³ + 48x² + 48x
= 12 (x³ + 4x² + 4x)
= 12x (x + 2)²
⇒ f’ (- 2) = 0
Also f(- 2) = 3(16) + 16(- 8) + 24(4) – 16 = 0
∴ (x + 2) is a factor of f(x) and f'(x).
∴ – 2 is a repeated root of f(x) = 0.
Now we divide f(x) by (x + 2) using synthetic division.

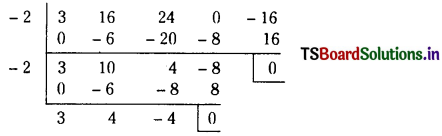
∴ f(x) = (x + 2) (x + 2) (3x² + 4x – 4)
Equation (1)
⇒ f(x) = 0
⇒ (x + 2) (x + 2) (3x² + 4x – 4) = 0
⇒ (x + 2) (x + 2) (3x – 2) (x + 2) = 0
⇒ x = – 2 or x = \(\frac{2}{3}\)
∴ The roots of given equation are – 2, – 2, – 2, \(\frac{2}{3}\).

III.
Question 1.
Solve x⁴ + x³ – 16x² – 4x + 48 = 0, given that the product of two of the roots is 6.
Solution:
Given equation is
x⁴ + x³ – 16x² – 4x + 48 = 0 ………….(1)
Let α, β, γ, δ be the roots
∴ x⁴ + x³ – 16x² – 4x + 48 = (x + α) (x – β) (x – γ) (x – δ) ……….(2)
∴ Sum of the roots α + β + γ + δ = – 1
and product of roots ⇒ αβγδ = 48 …………..(3)
Given product of two roots = 6
Let αβ = 6
∴ γδ = \(\frac{48}{\alpha \beta}\)
γδ = 8
Let α + β = a and γ + δ = b
Now (2)
⇒ x⁴ + x³ – 16x² – 4x + 48 = (x² – (α + β) x + αβ) (x² – (γ + δ) x + γδ)
⇒ x⁴ + x³ – 16x² – 4x + 48 = (x² – ax + 6) (x² – bx + 8)
Comparing like terms.
we get, a + b = – 1 and
8a – 6b = 5 ……………..(4)
⇒ 4a + 3b = 2 (5)
(5) ⇒ 4a + 3 (- 1 – a) = 2 (∵ from (4))
⇒ a = 5
∴ b = – 6
∴ x⁴ + x³ – 16x² – 4x + 48 = (x² – 5x + 6) (x² + 6x + 8)
= (x – 2) (x – 3) (x + 2) (x + 4)
∴ Equation (1),
⇒ (x – 2) (x – 3) (x + 2) (x + 4) = 0
∴ x = – 4; x = – 2 or x = 2 or x = 3
∴ The roots of the given equation are 2, 3, – 4, – 2.

Question 2.
Solve 8x⁴ – 2x³ – 27x² + 6x + 9 = 0 given that two roots have the same absolute value, but are opposite in sign.
Solution:
Given equation is
8x⁴ – 2x³ – 27x² + 6x + 9 = 0
⇒ x⁴ – \(\frac{1}{4} x^3-\frac{27}{8} x^2+\frac{3}{4} x+\frac{9}{8}\) = 0 ……………(1)
Let α, β, γ, δ be the roots of (1)
∴ Sum of the roots α + β + γ + δ = \(\frac{1}{4}\)
and product of roots αβγδ = \(\frac{9}{8}\)
But given two roots have same absolute value but are opposite sign.
Let α = – β
⇒ α + β = 0
∴ γ + δ = \(\frac{-1}{4}\)
Let αβ = a and γδ = b
Now(x – α) (x – β) = x² – (α + β)x + αβ
⇒ (x – α) (x – β) = x² + a …………(2)
Also (x – γ) (x – δ) = x² – (γ + δ)x + γδ
= (x – γ) (x – δ) = x² – \(\frac{1}{4}\) x + b ………….(3)
From (1), (2) and (3)
x⁴ – \(\frac{1}{4} x^3-\frac{27}{8} x^2+\frac{3}{4} x+\frac{9}{8}\) = (x² + a) (x² – \(\frac{1}{4}\) x + b)
Comparing like terms,
\(\frac{3}{4}=\frac{-a}{4}\) and ab = \(\frac{9}{8}\)
a = – 3
∴ b = \(\frac{9}{8(-3)}\)
b = \(\frac{-3}{8}\)
∴ (2) ⇒ (x – α) (x – β) = x² – 3
& (3) ⇒ (x – γ) (x – δ) = (x² – \(\frac{1}{4}\) x + \(\frac{3}{8}\))
⇒ \(\frac{1}{8}\) (8x² – 2x – 3)
⇒ (x – γ) (x – δ) = \(\frac{1}{8}\) (2x + 1) (4x – 3)
(x – γ) (x – δ) = (x + \(\frac{1}{2}\)) (x – \(\frac{3}{4}\))
∴ Equation (1)
(x² – 3) (x + \(\frac{1}{2}\)) (x – \(\frac{3}{4}\)) = 0
⇒ x = ± √3 or x = – \(\frac{1}{2}\) or x = \(\frac{3}{4}\)
∴ The roots of given equation are – √3, √3, – \(\frac{1}{2}\), \(\frac{3}{4}\).

Question 3.
Solve 18x³ + 81x² + 121x + 60 = 0 given that one root is equal to half the sum of the remaining roots.
Solution:
Given equation is
18x³ + 81x² + 121x + 60 = 0 ……………(1)
Let α, β, γ, δ be the roots
∴ Sum of roots, α + β + γ = \(\frac{-81}{18}=\frac{-9}{2}\)
αβ + βγ + γδ = \(\frac{121}{18}\)
and product of roots αβγ = \(\)
given one root is equal to halt of the sum of the remaining roots.
∴ Let α = \(\frac{\beta+\gamma}{2}\)
∴ α + 2α = \(\frac{-9}{2}\)
⇒ 3α = \(\frac{-9}{2}\)
⇒ α = \(\frac{-9}{2}\)
∴ x + \(\frac{3}{2}\) is a factor of 18x³ + 81x² + 121x + 60.
By synthetic division,

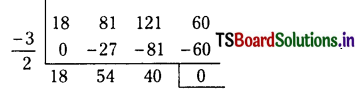
∴ 18x³ + 81x² + 121x + 60 = (x + \(\frac{3}{2}\)) (18x² + 54x + 40)
= (x + \(\frac{3}{2}\)) (9x² + 27x + 60)
∴ 18x³ + 81x² + 121x + 60 = 2 (x + \(\frac{3}{2}\)) (3x + 4) (3x + 5)
∴ Equation (1),
⇒ 2 (x + \(\frac{3}{2}\)) (3x + 4) (3x + 5) = 0
∴ x = \(\frac{-3}{2}\) or x = \(\frac{-4}{3}\) or x = \(\frac{-5}{3}\).
∴ The roots of given equation are \(\frac{-3}{2}\), \(\frac{-4}{3}\), \(\frac{-5}{3}\).

Question 4.
Find the condition In order that the equation ax⁴ + 4bx³ + 6cx² + 4dx + e = 0 may have two pairs of equal roots.
Solution:
Given equation is
ax⁴ + 4bx³ + 6cx² + 4dx + e = 0 ………………..(1)
Given (1) has two pairs of equal roots.
∴ Let α, α, β, β be the root of (1).
(1) ⇒ x⁴ + \(\frac{4 b}{a} x^3+\frac{6 c}{a} x^2+\frac{4 d}{a} x+\frac{e}{a}\) = 0

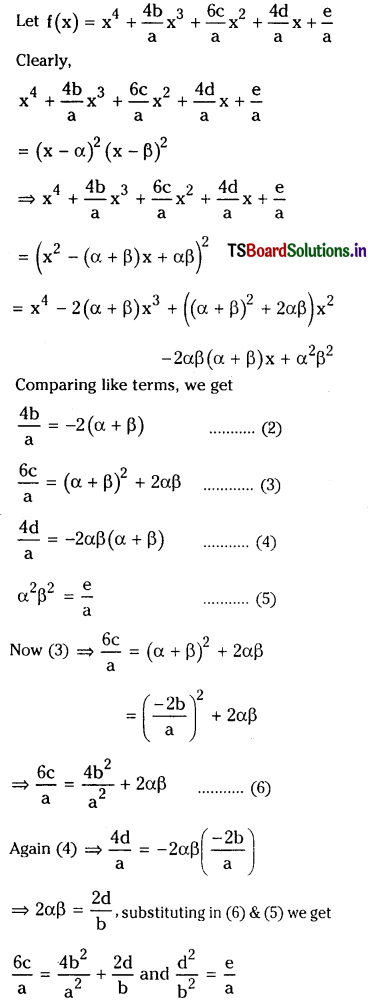
3abc = 2b³ + a²d and ad² = eb².
∴ The required conditions are 2b³ + a²d = 3abc and ad² = eb².

Question 5.
i) Show that x⁵ – 5x³ + 5x² – 1 = 0 has three equal roots and and this root.
ii) Find the repeated roots of x⁵ – 3x⁴ – 5x³ + 27x² – 32x + 12 = 0.
Solution:
i) Given equation is x⁵ – 5x³ + 5x² – 1 = 0
Let f(x) = x⁵ – 5x³ + 5x² – 1
f’(x) = 5x⁴ – 15x² + 10x
f”(x) = 20x³ – 30x + 10
f”(1) = 20 – 30 + 10 = 0
Similarly, f’(1) = 0 and f(1) = 0
∴ (x – 1) is a factor of f”(x), f’(x) & f(x).
Thus f(x) = 0 has three equal roots and it is ‘1’.

ii) Given equation is
x⁵ – 3x⁴ – 5x³ + 27x² – 32x + 12 = 0 …………(1)
Let f(x) = x⁵ – 3x⁴ – 5x³ + 27x² – 32x + 12
f’(x) = 5x⁴ – 12x³ – 15x² + 54x – 32
f’(1) = 5 – 12 – 15 + 54 – 32 = 0
Similarly f'(1) = 0 and f(1) = 0
∴ (x – 1) is a factor of f”(x), f'(x) & f(x).
Thus f(x) = 0 has three equal roots and it is ‘1’.
By synthetic division,

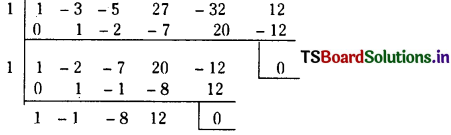
∴ f(x) = (x – 1)² (x³ – x² – 8x + 12)
Let g(x) = x³ – x² – 8x + 12
g’(x) = 3x² – 2x – 8
g’(2) = 3(4) – 2(2) – 8 = 0
and g(2) = 2³ – 2² – 8(2) + 12 = 0.
∴ (x – 2) is a factor of g(x) and g’(x).
∴ 2 is a multiple root of g(x) = 0.
By synthetic division,

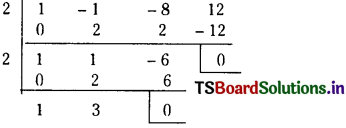
∴ g(x) = (x – 2)² (x + 3)
∴ f(x) = (x – 1)² (x – 2)² (x + 3)
The roots of given equation are 1, 1, 2, 2, 3.
Hence repeated roots are 1 and 2.

Question 6.
Solve the equation 8x³ – 20x² + 6x + 9 = 0 given that the equation has multiple roots.
Solution:
Given equation is 8x³ – 20x² + 6x + 9 = 0 …………..(1)
Let f(x) = 8x³ – 20x² + 6x + 9
f’(x) = 24x² – 40x + 6
= 2 (12x² – 20x + 3)
= 2 (2x – 3) (6x – 1)
\(f\left(\frac{3}{2}\right)=8\left(\frac{27}{8}\right)-20\left(\frac{9}{4}\right)+6\left(\frac{3}{2}\right)+9\)
= 27 – 45 + 9 + 9 = 0
∴ f(\(\frac{3}{2}\)) = 0
∴ f(x) and f'(x) has a common factor ‘2x – 3’.
∴ \(\frac{3}{2}\) is a multiple root of f(x) = 0.
By synthetic division,

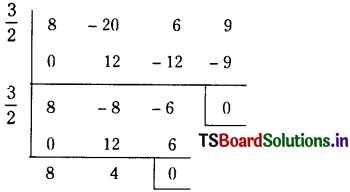
∴ 8x³ – 20x² + 6x + 9 = 0
(x – \(\frac{3}{2}\))² (8x + 4) = 0
⇒ x = \(\frac{3}{2}\) or x = \(\frac{-1}{2}\)
∴ The roots of given equation are \(\frac{-1}{2}\), \(\frac{3}{2}\), \(\frac{3}{2}\).