TS Inter 2nd Year Maths 2A Solutions Chapter 3 Quadratic Expressions Ex 3(b)

Students must practice this TS Intermediate Maths 2A Solutions Chapter 3 Quadratic Expressions Ex 3(b) to find a better approach to solving the problems.

TS Inter 2nd Year Maths 2A Solutions Chapter 3 Quadratic Expressions Exercise 3(b)

I.
Question 1.
If the quadratic equations ax² + 2bx + c = 0 and ax² + 2cx + b = 0, (b ≠ c) have a common root then show that a + 4b + 4c = 0.
Solution:
ax² + 2bx + c = 0
ax² + 2cx + c = 0
Let a be common root.
aα² + 2bα + c = 0
aα² + 2cα + b = 0
2α (b – c) + c – b = 0
(2α – 1) (b – c) = 0
α = \(\frac{1}{2}\)
\(\frac{a}{4}+\frac{2 b}{2}\) + c = 0
a + 4b + 4c = 0.

Question 2.
If x² – 6x + 5 = 0 and x² – 12x + p = 0 have a common root, then find p.
Solution:
x² – 6x + 5 = 0
(x – 5) (x – 1) = 0
x = 1, 5
Now x² – 12x + p = 0, can have 1 or 5 as root then 1 – 12 + p = 0
p = 11 (or)
25 – 60 + p = 0
p = 35.

Question 3.
If x² – 6x + 5 = 0 and x² – 3ax + 35 = 0 have a common root, then find a.
Solution:
(x² – 6x + 5) = 0
(x – 5) (x – 1) = 0
x = 5, 1
Now, 5, 1 satisfy
x² – 3ax + 35 = 0
25 – 15a + 35 = 0
60 = 15a
a = 4
1 – 3a + 35 = 0
3a = 36
a = 12.

Question 4.
If the equations x² + ax + b = 0 and x² + cx + d = 0 have a common root and the first equation have equal roots, then prove that 2 (b + d) = ac.
Solution:
x² + ax + b = 0
x² + cx + d = 0
x² + ax + b = 0 have equal roots.
⇒ a² – 4b = 0
a² = 4b
x² + ax + b = 0
x² + cx + d = 0
α (a – c) + b – d = 0
as 2α = – a
α = \({-a}{2}\)
\(\frac{a^2}{4}+c\left(\frac{-a}{2}\right)\) + d = 0
a² – 2ac + 4d = 0
4b + 4d = 2ac
or (b + d) = ac.

Question 5.
Discuss the signs of the following quadratic expressions when x is real.
i) x² – 5x + 4
ii) x² – x + 3
Solution:
i) f(x) = x² – 5x + 4
f(x) = (x – 4) (x – 1)
y = \(\left(x-\frac{5}{2}\right)^2+4-\frac{25}{4}\)
y = \(\left(x-\frac{5}{2}\right)^2-\frac{9}{4}\)
y + \(\frac{9}{4}\) = \(\left(x-\frac{5}{2}\right)^2\)

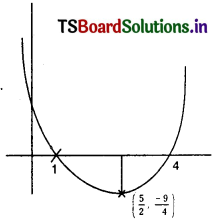
f(x) < 0
1 < x < 4 f(x) > 0
x > 4 and x < 1
(- ∞ < x < 1) ∪ (4 < x < ∞).

ii) x² – x + 3
f(x) = x² – x + 3
= \(\left(x-\frac{1}{2}\right)^2+3-\frac{1}{4}\)
y = \(\left(x-\frac{1}{2}\right)^2+\frac{11}{4}\)
y – \(\frac{11}{4}\) = \(\left(x-\frac{1}{2}\right)^2\)
Now discriminant = 1 – 12 < 0

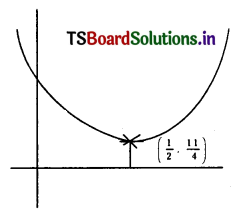
f(x) > 0 ∀ x ∈ Real numbers.

Question 6.
For what values of x the following expressions are positive?
i) x² – 5x + 6
ii) 3x² + 4x + 4
iii) 4x – 5x² + 2
iv) x² – 5x + 14
Solution:
i) f(x) = x² – 5x + 6
f(x) > 0
x² – 5x + 6 > 0
(x – 3) (x – 1)> 0
x > 3 or x < 1
(- ∞ < x < 1) ∪ (3 < x < ∞)

ii) 3x² + 4x + 4
f(x) = 3x² + 4x + 4
f(x) > 0
3x² + 4x + 4> 0
x² + \(\frac{4}{3}\)x + \(\frac{4}{3}\) > 0
\(\left(x+\frac{2}{3}\right)^2+\frac{4}{3}-\frac{4}{9}\) > 0
\(\left(x+\frac{2}{3}\right)^2+\frac{8}{9}\) > 0 ∀ x ∈ Real numbers.

iii) f(x) = 4x – 5x² + 2
= [5x² – 4x – 2]

iv) f(x) = x² – 5x + 14
f(x) > 0
\(\left(x-\frac{5}{2}\right)^2+14-\frac{25}{4}\) > 0
\(\left(x-\frac{5}{2}\right)^2+\frac{31}{4}\) > 0.

Question 7.
For what values of x, the following expres¬sions are negative ?
i) x² – 7x + 10
ii) 15 + 4x – 3x²
iii) 2x² + 5x – 3
iv) x² – 5x – 6
Solution:
i) f(x) = x² – 7x + 10
f(x) < 0
(x – 5) (x – 2) < 0
2 < x < 5.

ii) f(x) = 15 + 4x – 3x²
f(x) < 0
15 + 4x – 3x² < 0
3x² – 9x + 5x – 15 > 0
3x (x – 3) + 5 (x – 3) > 0
(x – 3) (3x + 5) > 0
x > 3, x < \(\frac{-5}{3}\)
(- ∞ < x < \(\frac{-5}{3}\)) ∪ (3 < x < ∞).

iii) if(x) = 2x² + 5x – 3
f(x) < 0
2x² + 5x – 3 < 0
2x² + 6x – x – 3 < 0
2x (x + 3) – 1 (x + 3) < 0
(2x – 1) (x + 3) < 0
– 3 < x < \(\frac{1}{2}\).

iv) f(x) = x² – 5x – 6
f(x) < 0
x² – 5x – 6 < 0
(x – 6) (x + 1) < 0
– 1 < x < 6.

Question 8.
Find the changes in the sign of the following expressions and find their extreme values.
i) x² – 5x + 6
ii) 15 + 4x – 3x²
Solution:
i) f(x) = x² – 5x + 6
= (x – 3) (x – 2)
f(x) < 0
2 < x < 3 and f(x) > 0
(- ∞ < x < 2) (3 < x < ∞)
y = \(\left(x-\frac{5}{2}\right)^2+\frac{6-25}{4}\)
y_min. = \(\frac{-1}{4}\)

ii) f(x) = 15 + 4x – 3x²
f(x) <0
15 + 4x – 3x² < 0
3x² – 4x – 15 < 0
3x² – 9x + 5x – 15 < 0
3x (x – 3) 5 (x – 3) < 0
(x – 3) (3x + 5) < 0
\(\frac{-3}{5}\) < x < 3 f(x) > 0
(- ∞ < x < \(\frac{-3}{5}\)) ∪ (3 < x < ∞)
y = 15 + 4x – 3x²

Question 9.
Find the maximum or minimum of the following expressions as x varies over R.
i) x² – x + 7
ii) 12x – x² – 32
iii) 2x+ 5 – 3x²
iv) ax² + bx + a (a, b ∈ R and a ≠ 0)
Solution:
i) y = x² – x + 7
y = (x – \(\frac{1}{2}\))² – \(\frac{1}{4}\) + 7
y = (x – \(\frac{1}{2}\))² + \(\frac{27}{4}\)
y_min = \(\frac{27}{4}\)

ii) y = 12x – x² – 32
y = – [x² – 12x + 32]
= – [(x – 6)² – 36 +32]
y = – [x – 6]² + 4
y_max = 4

iii) f(x) = 2x + 5 – 3x²
y = – 3 [x² – \(\frac{2}{3}\) x – \(\frac{5}{3}\)]
= – 3 \(\left[\left(x-\frac{1}{3}\right)^2-\frac{1}{9}-\frac{15}{9}\right]\)
= – 3 \(\left(x-\frac{1}{3}\right)^2+\frac{16}{3}\)
y_max = \(\frac{16}{3}\)

iv) f(x) = ax² + bx + a

II.
Determine the range of the following expressions.
Question 1.
i) \(\frac{x^2+x+1}{x^2-x+1}\)
ii) \(\frac{x+2}{2 x^2+3 x+6}\)
iii) \(\frac{(x-1)(x+2)}{x+3}\)
iv) \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\)
Solution:
\(\frac{x^2+x+1}{x^2-x+1}\)
yx² – yx + y = x² + x + 1
x² (y² – 1) + x (- y – 1) + y – 1 = 0
Discriminant ≥ 0
(- y- 1)² – 4(y – 1) (y – 1) ≥ 0
(y² + 2y + 1) – 4 (y² – 2y + 1) ≥ 0
– 3y² +10y – 3 ≤ 0
3y² – 10y + 3 ≤ 0
3y² – 9y – y + 3 ≤ 0
3y (y – 3) – 1 (y – 3) ≤ 0
(3y – 1) (y – 3)≤ 0
\(\frac{1}{3}\) ≤ y ≤ 3.

ii) y = \([\frac{x+2}{2 x^2+3 x+6}/latex]
2x²y + 3xy + 6y – x – 2 = 0
x² (2y) + x (3y – 1) + 6y – 2 = 0
Discriminant ≥ 0
(3y – 1)² – 4 (2y) (6y – 2) ≥ 0
9y² – 6y + 1 – 48y² + 16y ≥ 0
– 39y² + 10y + 1 ≥ 0
39y² – 10y – 1 ≥ 0
39y² – 13y + 3y – 1 ≤ 0
13y (3y – 1) + (3y – 1) ≤ 0
(13y – 1) (3y – 1) ≤ 0
[latex]-\frac{1}{13}\) ≤ y ≤ \(\frac{1}{3}\).

iii) y = \(\frac{(x-1)(x+2)}{x+3}\)
y = \(\frac{x^2+x-2}{x+3}\)
yx + 3y = x² + x – 2
x² + x(1 – y) – 2 – 3y = 0
Discriminant ≥ 0
(1 – y)² + 4(2 + 3y) ≥ 0
y² – 2y + 1 + 8 + 12y ≥ 0
y² + 10y + 9 ≥ 0
(y + 1) (y + 9) ≥ 0
y ≥ – 1 or y ≤ – 9
(- ∞ < y ≤ – 9) ∪ (- 1 ≤ y < ∞)

iv) y = \(\frac{2 x^2-6 x+5}{x^2-3 x+2}\)
y (x² – 3x . 2) = 2x² – 6x + 5
x² (y – 2) + x(- 3y + 6) + 2y – 5 = 0
Discriminant ≥ 0
(6 – 3y)² – 4(y – 2) (2y – 5)≥0
9y² – 36y + 36 – 8y² + 36y – 40 ≥ 0
y² -4 ≥ 0
(y – 2) (y + 2) ≥ 0
y ≥ 2 or y ≤ – 2
(- ∞ < y ≤ – 2) ∪ (2 ≤ y < ∞)

Question 2.
Prove that \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\) does not lie between 1 and 4 if x ∈ Real number.
Solution:
y = \(\frac{1}{3 x+1}+\frac{1}{x+1}-\frac{1}{(3 x+1)(x+1)}\)
y = \(\frac{4 x+1}{3 x^2+4 x+1}\)
3yx² + x(4y – 4) + y – 1 = 0
Discriminant ≤ 0
[4 (y – 1)]² – 4 . 3y (y- 1) ≤ 0
16 (y- 1)² – 12y(y- 1) ≤ 0
4(y – 1) [4(y – 1) – 3y)]≤ 0
4(3 – 1) [y – 4] ≤ 0
(y – 1) (y – 4) ≤ 0
⇒ y ≤ 4 or y ≥ 1.

Question 3.
If x is real, prove that \(\frac{x}{x^2-5 x+9}\) lies between \(\frac{-1}{11}\) and 1.
Solution:
y = \(\frac{x}{x^2-5 x+9}\)
y (x² – 5x + 9) = x
x²y + x(- 5y – 1) + 9y = 0
Discriminant ≤ 0
(- 5y – 1)² – 4 . 9y² ≥ 0
25y² + 10y + 1 – 36y² ≥ 0
– 11y² + 10y + 1 ≥ 0
11y² – 10y – 1 ≤ 0
11y² – 11y + y – 1 ≤ 0
11y (y- 1) + (y- 1) ≤ 0
(y – 1) (11y + 1) ≤ 0
\(\frac{-1}{11}\) ≤ y ≤1.

Question 4.
If the expression \(\frac{x-p}{x^2-3 x+2}\) takes all values of x ∈ R, then find the bounds for p.
Solution:
y = \(\frac{x-p}{x^2-3 x+2}\)
y(x² – 3x + 2) = x – p
x²y + x(- 3y – 1) + p = 0
Discriminant ≥ 0
(- 3y- 1)² – 4y(2y + p) ≥ 0
9y² + 6y + 1 – 8y² – 4p ≥ 0
y² + y(6 – 4p)+ 1 ≥ 0
Discriminant< 0
(6 – 4p)² – 4 < 0
16p² – 48p + 36 – 4< 0
16p² – 48p + 32 < 0
p² – 48p + 32 < 0
p² – 3p + 2 < 0
(p – 2) (p – 10)
1 < p < 2.

Question 5.
If c² ≠ ab and the roots of (c² – ab) x² – 2 (a² – bc) x + (b² – ac) = 0 are equal, then show that a³ + b³ + c³ = 3abc or a = 0.
Solution:
Roots are equal = Discriminant = 0
4 (a² – bc)² – 4 (c² – ab) (b² – ac) = 0
a⁴ + b²c² – 2a²bc – b²c² + c³a + b³a – a²bc = 0
a⁴ – 2a²bc + c3a. b3a – a²bc = 0
a (a³ + b³ + c³ – 3abc = 0
a³ + b³ + c³ – 3abc = 0 or a = 0