TS Inter 1st Year Maths 1B Solutions Chapter 10 Applications of Derivatives Ex 10(f)

Students must practice this TS Inter 1st Year Maths 1B Study Material Chapter 10 Applications of Derivatives Ex 10(f) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(f)

Question 1.
Verify Rolle’s theorem for the following functions. (V.S.A.Q.)
(i) x² – 1 on [-1, 1]
Answer:
Let f(x) = x² defined on [-1, 1].
Since the function f(x) is a polynomial, it is continuous on [-1, 1] and differentiable on (-1, 1)
Also f(1) = 1 – 1 = 0, f(- 1) = (- 1)² – 1 = 0
∴ f (-1) = f (1). Hence f satisfy all conditions of Rolle’s theorem. Now we have to find a point c ∈ (-1,1) such that f'(c) = 0, f'(x) = 2x and f'(c) = 0 ⇒ 2c = 0
⇒ c = 0 ∈ (-1, 1)
Hence Rolle’s theorem is verified.

(ii) sin x – sin 2x on [0, π]
Answer:
Let f(x) = sin x – sin 2x defined over [0, π] f is continuous over [0, π] and differentiable over (0, π).
Also f(0) = 0 and f(π) = sin π – sin 2π = 0
∴ f(0) = f(π) = 0.
Hence f satisfy conditions of Rolle’s theorem’.
Also f'(x) = cos x – 2 cos 2x and f’ (c) = 0
⇒ cos c – 2 cos 2c = 0
⇒ cos c = 2 (2 cos²c – 1)
⇒ 4 cos²c – cos c – 2 = 0

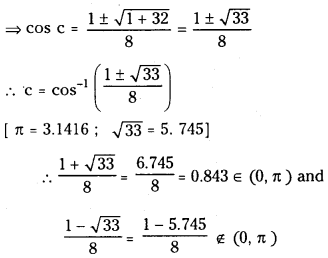
Hence conditions of Rolle’s theorem are verified.

(iii) log (x² + 2) – log 3; over [-1, 1]
Answer:
f(x) = log (x² + 2) – log 3
This function is continuous over [-1,1] and differentiable over (-1,1)
f (-1) = log (1 + 2) – log 3 = 0
f(1) = log 3 – log 3 = 0
f (-1) = f (1)
Hence f satisfy all the conditions of Rolle’s theorem. So we have to find c ∈ (-1,1)
such that f’ (c) = 0 and f’ (c) = 0
⇒ c = 0 ∈ (-1, 1)
So Rolle’s theorem is verified.

Question 2.
It is given that Rolle’s theorem holds for the function f(x) = x³ + bx² + ax on [1, 3] with c = 2 + \(\frac{1}{\sqrt{3}}\). Find the values of a and b.
Answer:
Given that f(x) = x³ + bx² + ax defined over [1, 3] satisfy all the conditions of Rolle’s theorem.
∴ f ’(x) = 3x² + 2bx + a

b = -6, and b² – 3a = 3
⇒ 36 – 3a = 3 ⇒ a = 11
Hence a = 11 and b = – 6

Question 3.
Show that there is no real number k, for which the equation x² – 3x + k = 0 has two distinct roots in [0, 1]. (S.A.Q.)
Answer:
Let f(x) = x² – 3x + k and suppose there exists two different roots α, β (α < β). Since f is a polynomial in x, it is continuous over [0, 1] and differentiable in (0, 1). f is continuous over [a, 3] and differentiable in (a, β).
Also f(α) = α² – 3α + k = 0 and
f(β) = β² – 3β + k = 0
f(α) = f(β) = o :
f satisfy the conditions of Rolle’s theorem.
Also f'(c) = 0 ⇒ 3c² – 3 = 0
⇒ c² = 1
⇒ c = ± 1
This is a contradiction since
0 < α < c < β < 1
Hence there does not exists roots α, β in (0, 1).
So, there is no real number k for which the equation x² – 3x + k = 0 has distinct roots in[0, 1]

Question 4.
Find a point on the graph of the curve y = (x – 3)² where the tangent is parallel to the chord joining (3, 0) and (4, 1). (S.A.Q.)
Answer:
Let the points be A (3, 0) and B (4, 1)
∴ Slope of chord AB = \(\frac{1-0}{4-3}\) = 1
Given y = (x – 3)²
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 2(x – 3)
Slope of the chord 2 (x – 3) = 1
⇒ 2x = 7 ⇒ x = \(\frac{7}{2}\)
∴ y = (x – 3)² = (\(\frac{7}{2}\) – 3) = \(\frac{1}{4}\)
The point on the curve = \(\left(\frac{7}{2}, \frac{1}{4}\right)\)

Question 5.
Find a point on the graph of the curve y = x³ where the tangent is parallel to the chord joining (1, 1) and (3, 27). (S.A.Q.)
Answer:
Let the points be A (1, 1) and B (3, 27)
Slope of chord AB = \(\frac{27-1}{3-1}=\frac{26}{2}\) = 13

Question 6.
Find ‘c’ so that f'(c) = \(\frac{f(b)-f(a)}{b-a}\) in the following cases. (S.A.Q)
(i) f(x) = x² – 3x – 1; a = \(\frac{-11}{7}\), b = \(\frac{13}{7}\)
Answer:

Question 7.
Verify the Rolle’s theorem for the function (x² – 1) (x – 2) on [- 1, 2]. Find a point in the interval where the derivative vanishes. (S.A.Q.)
Answer:
Let f(x) = (x² – 1) (x – 2)
= x³ – 2x² – x + 2 defined over [-1, 2] f being a polynomial in ‘x’, it is continuous over [-1, 2] and differentiable over (- 1, 2) f (- 1) = 0, f(2) = 0 f(-1) = f(2)
∴ f satisfy all the conditions of Rolle’s theorem.
f'(x) = 3x² – 4x – 1
and f'(c) = 0 ⇒ 3c² – 4c – 1 = 0

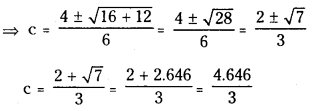
= 1.549 ∈ (-1, 2)
Rolle’s theorem is verified.

Question 8.
Verify the conditions of the Lagrange’s mean value theorem for the following functions. In each case find a point ‘c’ in the interval as stated by the theorem. (S.A.Q.)
(i) x² – 1 on [2, 3]
Answer:
Let f(x) = x² – 1 defined over [2, 3]. This being a polynomial in x, continuous on [2,3] and djfferentiable over (2,3). So by Lagrange’s mean value theorem there exists a point ‘c’ ∈ (2, 3) such that
f'(c) = \(\frac{\mathrm{f}(3)-\mathrm{f}(2)}{3-2}\)
f'(x) = 2x ⇒ f'(c) = 2c f(3) = 8, 1(2) = 3
∴ 2c = \(\frac{8-3}{1}\) = 5 ⇒ c = \(\frac{5}{2}\) ∈ (2, 3)

(ii) sin x – sin 2x on [0, π]
Answer:
Let f(x) = sin x – sin 2x defined over [0, π]. This is continuous on [0, π] and differentiable over (0, π) since
f’ (x) = cos x – 2 cos 2x exists for all x ∈ (0, π). So by Lrgrange s mean value theorem
f'(c) = \(\frac{\mathrm{f}(\pi)-\mathrm{f}(0)}{\pi-0}\), f(π) = 0, f(0) = 0
∴ cos c – 2 cos 2c = \(\frac{0}{\pi}\) =0
⇒ cos c – 2 cos 2c = 0
⇒ cos c – 2 (2 cos² c – 1) = 0
⇒ 4cos² c – cos c – 2 = 0
⇒ cos c = \(\frac{1 \pm \sqrt{1+32}}{8}=\frac{1 \pm \sqrt{33}}{8}\)
∴ c ∈ cos^-1\(\left(\frac{1+\sqrt{33}}{8}\right)\) ∈ (0, π)

(ii) log x on [1, 2]
Let f(x) = log x defined over [1,2]
This is continuous over [1, 2] and differentiable over (1, 2) since

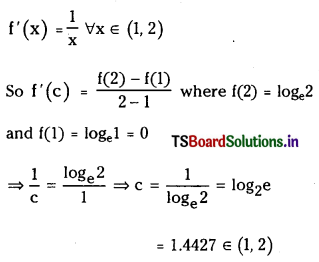
Hence Lagrange’s mean value theorem is satisfied.