TS 10th Class Maths Solutions Chapter 8 Similar Triangles Optional Exercise

Students can practice TS Class 10 Maths Solutions Chapter 8 Similar Triangles Optional Exercise to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 8 Similar Triangles Optional Exercise

Question 1.
In the given figure, \(\frac{\mathrm{Q T}}{\mathrm{P R}}\) = \(\frac{\mathrm{QR}}{\mathrm{QS}}\) and ∠1 = ∠2. Prove that ∆PQS ~ ∆TQR.

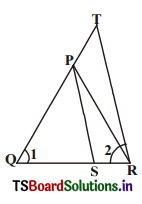
Solution:
Given : \(\frac{\mathrm{Q T}}{\mathrm{P R}}\) = \(\frac{\mathrm{QR}}{\mathrm{QS}}\) // ∠1 = ∠2
R.T.P : ∆PQS ~ ∆TQR
Proof : In ∆PQR; ∠l = ∠2
Thus, PQ = PR
[∵ Sides opp. to equal angles are equal]
∴ \(\frac{\mathrm{QT}}{\mathrm{PR}}\) = \(\frac{\mathrm{QR}}{\mathrm{QS}}\)
⇒ \(\frac{\mathrm{QT}}{\mathrm{PQ}}\) = \(\frac{\mathrm{QR}}{\mathrm{QS}}\)
i.e., the lines PS divides the two sides QT and QR of ∆TQR in the same ratio.
Hence, PS // TR.
[∵ If a line join of any two points on any two sides of triangle divides the two sides in the same ratio, then the line is parallel to the third side]
Hence, PS // TR (Converse of B.RT)
Now in ∆PQS and ∆TQR.
∠QPS = ∠QTR
[∵ ∠R ∠T are corresponding angles for PS // TR]
∠QSP = ∠QRT
[∵ ∠S, ∠R are corresponding angles for PS // TR]
∠Q = ∠Q (Common)
∴ ∆PQS ~ ∆TQR (by A.A.A similarity)

Question 2.
Ravi is 1.82m tall. He wants to find the height of a tree in his backyard. From the tree’s base he walked 12.20 m. along the tree’s shadow to a position where the end of his shadow exactly overlaps the end of the tree’s shadow. He is now 6.10m from the end of the shadow. How tall is the tree?

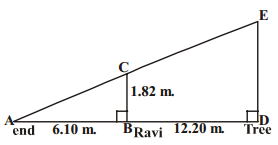
Solution:
Given :
Height of Ravi ‘BC’ = 1.82 m.
Distance of Ravi from the foot of the tree BD
= 12.2 m
Length of the shadow of Ravi = AB
= 6.10 m
Let DE represent the tree.
From the figure, ∆ABC ~ ∆ADE.
Thus, \(\frac{\mathrm{AB}}{\mathrm{AD}}\) = \(\frac{\mathrm{BC}}{\mathrm{DE}}\) = \(\frac{\mathrm{AC}}{\mathrm{AE}}\)
[∵ Ratio of corresponding sides of two similar triangles are equal]
\(\frac{6.10}{6.10+12.20}\) = \(\frac{1.82}{\mathrm{DE}}\)
DE = \(\frac{1.82 \times 18.30}{6.10}\) = 5.46 m
∴ Thus the height of the tree = 5.46 m.

Question 3.
The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where ‘P’ is any point on side AB. Prove that CQ × PQ = QA × QD.
Solution:

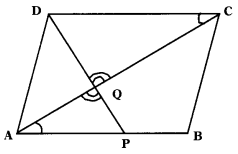
Given : □ ABCD is a parallelogram.
P is a point on AB.
DP and AC intersect at Q.
R.T.P : CQ . PQ = QA . QD
Proof : In ∆CQD, ∆AQP
∠QCD = ∠QAP
∠CQD = ∠AQP
∴ ∠QDC = ∠QPA
(∵ Angle sum property of triangles)
Thus, ∆CQD ~ ∆AQP by A.A.A similarity condition.
∴ \(\frac{\mathrm{CQ}}{\mathrm{AQ}}\) = \(\frac{\mathrm{QD}}{\mathrm{QP}}\) = \(\frac{\mathrm{CD}}{\mathrm{AP}}\)
[∵ Ratio of corresponding sides of similar triangles are equal]
\(\frac{\mathrm{CQ}}{\mathrm{AQ}}\) = \(\frac{\mathrm{QD}}{\mathrm{QP}}\)
CQ . PQ = QA . QD [Q.E.D]

Question 4.
∆ABC and ∆AMP are two right triangles right angled at B and M respectively. Prove that
(i) ∆ABC ~ ∆AMP
(ii) \(\frac{\mathrm{CA}}{\mathrm{PA}}\) = \(\frac{\mathrm{BC}}{\mathrm{MP}}\)

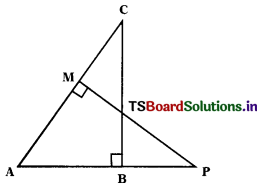
Solution:
Given : ∆; ∠B = 90°.
∆AMP; ∠M = 90°
R.T.P : i) ∆ABC ~ ∆AMP
Proof : In ∆ABC and ∆AMP
∠B = ∠M (each 90° given)
∠A = ∠A (common)
Hence, ∠C = ∠P [∵ Angle sum property of triangles]
∴ ∆ABC ~ ∆AMP (by A.A.A. similarity)

ii) ∆ABC ~ ∆AMP (already proved)
\(\frac{\mathrm{AB}}{\mathrm{AM}}\) = \(\frac{\mathrm{BC}}{\mathrm{MP}}\) = \(\frac{\mathrm{CA}}{\mathrm{PA}}\)
[∵ Ratio of corresponding sides of similar tri-angles are equal]
∴ \(\frac{\mathrm{CA}}{\mathrm{PA}}\) = \(\frac{\mathrm{BC}}{\mathrm{MP}}\)

Question 5.
An aeroplane leaves an airport and flies due north at a speed of 1000 kmph. At the same time another aeroplane leaves the same airport and flies due west at a speed of 1200 kmph. How far apart will the two planes be after 1\(\frac{1}{2}\) hour ?
Solution:

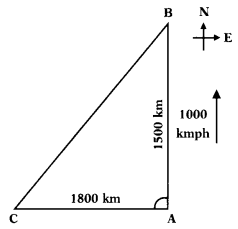
Given : Speed of the first plane due north = 1000 kmph.
Speed of the second plane due west = 1200 kmph.
Distance = Speed × Time Distance travelled by the first plane in
1\(\frac{1}{2}\) hrs = 1000 × 1\(\frac{1}{2}\) = 1000 × \(\frac{3}{2}\)
= 1500 km.
Distance travelled by the second plane in
1\(\frac{1}{2}\) hrs = 1200 × \(\frac{3}{2}\) = 1800 km.
From the figure, ∆ABC is a right triangle;
∠A = 90°.
∴ AB² + AC² = BC² [Pythagoras theorem]
1500² + 1800² = BC²
2250000 + 3240000 = BC²
∴ BC = \(\sqrt{5490000}\)
= 100 × \(\sqrt{549}\) m ☐ 100 × 23.43 ☐ 2243 km.

Question 6.
In a right triangle ABC right angled at C. P and Q are points on sides AC and CB respectively which divide these sides in the ratio of 2 : 1.
Prove that
(i) 9AQ² = 9AC² + 4BC²
(ii) 9BP² = 9BC² + 4AC²
(iii) 9(AQ² + BP²) = 13AB²
Solution:

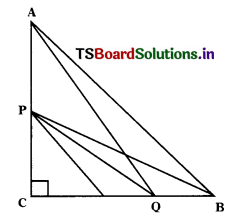
Given : In ∆ABC; ∠C = 90°
R.T.P : i) 9AQ² = 9AC² + 4BC²
Proof : In ∆ACQ; ∠C = 90°
AC² + CQ² = AQ²
[side² + side² = hypotenuse²]
AQ² = AC² + \(\left(\frac{2}{3} \mathrm{BC}\right)^2\)
[∵ Q divides CB in the ratio 2:1; CQ = \(\frac{2}{3}\) BC]
AQ² = AC² + \(\frac{4}{9}\) BC²
AQ² = \(\frac{9 \mathrm{AC}^2+4 \mathrm{BC}^2}{9}\)
⇒ 9AQ² = 9AC² + 4BC²

ii) 9BP² = 9BC² + 4AC²
Proof : In ∆PCB,
PB² = PC² + BC² [Pythagoras theorem]
PB² = \(\left(\frac{1}{3} \mathrm{AC}\right)^2\) + BC²
PB² = \(\frac{\mathrm{AC}^2}{9}\) + BC²
PB² = \(\frac{\mathrm{AC}^2+9 \mathrm{BC}^2}{9}\)
⇒ 9PB² = 9BC² + AC²
!! If we take P on CA, in the ratio 2 : 1 then we get
BP² = PC² + BC²
BP² = \(\left(\frac{2}{3} \mathrm{AC}\right)^2\) + BC²
BP² = \(\frac{4}{9}\) AC² + BC²
BP² = \(\frac{4 \mathrm{AC}^2+9 \mathrm{BC}^2}{9}\)
9BP² = 4AC² + 9BC²

iii) 9(AQ² + BP²) = 13 AB²
Proof : In ∆ABC,
AC² + BC² = AB² [Pythagoras theorem]
Also, from (i) and (ii),
9AQ² = 9AC² + 4BC²
9BP² = 9BC² + 4AC²
On adding
we get, 9AQ² + 9BP² = 13AC² + 13BC²
9(AQ² + BP²) = 13(AC² + BC²) [Q.E.D]