TS 10th Class Maths Solutions Chapter 3 Polynomials Ex 3.4

Students can practice TS 10th Class Maths Solutions Chapter 3 Polynomials Ex 3.4 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 3 Polynomials Exercise 3.4

Question 1.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following.
i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2
ii) p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x
iii) p(x) = x⁴ – 5x + 6 and g(x) = 2 – x²
Solution:
i) p(x) = x³ – 3x² + 5x – 3 and
g(x) = x² – 2
The given polynomials are in standard form.

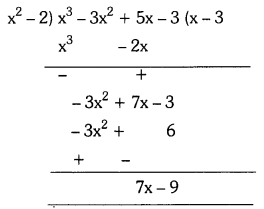
The degree of x² – 2 is 2.
The degree of 7x – 9 is 1.
∴ We stop here since the degree of (7x – 9) < degree of (x² – 2)
So, the quotient is x – 3 and the remainder is 7x – 9.

ii) p(x) = x⁴ – 3x² + 4x + 5,
g(x) = x² + 1 – x
p(x) = x⁴ – 3x² + 4x + 5, it is in standard form.
g(x) = x² + 1 – x, it is not in standard form. Writing it in standard form, we have x² – x + 1. Now we apply the division algorithm to the given polynomials.

The degree of x² – x + 1 is 2
The degree of 8 is 0.
∴ We stop here since the degree of (8) < degree of (x² – x + 1)
So, the quotient is x² + x – 3 and the remainder is 8.

iii) p(x) = x⁴ – 5x + 6 and g(x) = 2 – x²
p(x) = x⁴ – 5x + 6 → it is in standard form
g(x) = 2 – x² → it is not in standard form writing it in standard form, we have -x² + 2.
Now we apply the division algorithm to the given polynomials

The degree of -x² + 2 is 2 and that of (-5x + 10) is 1
The degree of (-x² + 2) > degree of (-5x + 10)
So, we stop here
So, the quotient is -x² – 2 and the remainder is -5x + 1o.

Question 2.
Check in which case the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:
i) t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12
ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
Solution:
Divide the second polynomial by the first polynomial. If the remainder is zero, then the first polynomial is a factor of the second one. The given polynomials are in standard form.
i)

Since the remainder is ‘0’, t² – 3 is a factor of 2t⁴ + 3t³ – 2t² – 9t – 12.

ii)

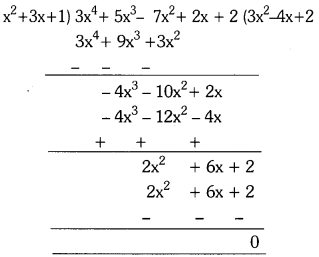
Since the remainder is ‘0’, x² + 3x + 1 is a factor of 3x⁴ + 5x³ – 7x² + 2x + 2.

iii)

Here, the remainder is 2.
∴ x³ – 3x + 1 is not a factor of x⁵ – 4x³ + x² + 3x + 1.
x⁵ – 4x³ + x² + 3x + 1

Question 3.
Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are
\(\sqrt{\frac{5}{3}}\) and –\(\sqrt{\frac{5}{3}}\).
Solution:
The given polynomial is
3x⁴ + 6x³ – 2x² – 10x – 5.
Two of its zeroes are \(\sqrt{\frac{5}{3}}\) and –\(\sqrt{\frac{5}{3}}\).
∴ [x – \(\sqrt{\frac{5}{3}}\)][x + \(\sqrt{\frac{5}{3}}\)] = [x² – \(\sqrt{\frac{5}{3}}\)] is a factor of the given polynomial.
Now, we apply the division algorithm to the given polynomial & x² – \(\frac{5}{3}\).

3x⁴ + 6x³ – 2x² – 10x – 5 = (x² – \(\frac{5}{3}\)) (3x² + 6x + 3)
3x² + 6x + 3 = 3(x² + 2x + 1) = 3(x + 1)²
So, the zeroes of 3(x + 1)² are -1 and -1.
Therefore, the zeroes of the given polynomial are and \(\sqrt{\frac{5}{3}}\) and –\(\sqrt{\frac{5}{3}}\), -1 and -1

Question 4.
On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and -2x + 4 respectively. Find g(x).
Solution:
By division algorithm, we have
p(x) = g(x) × q(x) + r(x)
g(x) × q(x) = p(x) – r(x)
g(x) × (x – 2) = x³ – 3x² + x + 2 – (-2x + 4)
= x³ – 3x² + x + 2 + 2x – 4
= x³ – 3x² + 3x – 2
∴ g(x) = (x³ – 3x² + 3x – 2) ÷ (x – 2)

∴ g(x) = x² – x + 1

Question 5.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
i) deg p(x) = deg q(x)
ii) deg q(x) = deg r(x)
iii) deg r(x) = 0
Solution:
i) p(x) = 6x² – 12x + 15, g(x) = 3,
q(x) = 2x² – 4x + 5, r(x) = 0
ii) p(x) = x³ + 2x² + x – 6, g(x) = x² + 2
q(x) = x + 2, r(x) = -x – 10
iii) p(x) = x³ + 5x² – 3x – 10, g(x) = x² – 3
q(x) = x + 5, r(x) = 5