TS 10th Class Maths Solutions Chapter 14 Statistics Ex 14.2

Students can practice 10th Class Maths Textbook SSC Solutions Telangana Chapter 14 Statistics Ex 14.2 to get the best methods of solving problems.

TS 10th Class Maths Solutions Chapter 14 Statistics Exercise 14.2

Question 1.
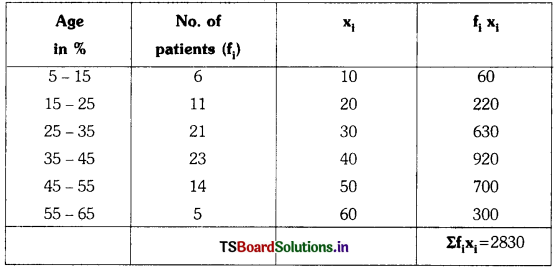
The following table shows the ages of the patients admitted in a hospital during a year :

Age (in years)	5-15	15-25	25-35	35-45	45-55	55-65
Number of patients	6	11	21	23	14	5

Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency. (AS₃, AS₄)
Solution:
Maximum number of patients joined in the age group 35 – 45
∴ Modal class is 35 – 45.
Lower limit of the modal class ‘l’ = 35
class size, h = 10
Frequency of modal class. f₁ = 23
Frequency of the class preceding the modal class f₀ = 21
Frequency of the class succeding the modal class f₂ = 14

∴ Mode = l + \(\frac{\left(f_1-f_0\right)}{2 f_1-f_0-f_2}\) × h
= 35 + \(\left[\frac{23-21}{2 \times 23-21-14}\right]\) × 10
= 35 + \(\left[\frac{2}{46-35}\right]\) × 10
= 35 + \(\frac{2}{11}\) × 10 = 35 + 1.81818 ….
= 36.8 years

Mean \(\overline{\mathrm{x}}\) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) = \(\frac{2830}{80}\) = 35.37 years.

Interpretation : Mode age is 36.8 years, Mean age = 35.37 years.
Maximum number of patients admitted in the hospital are the age 36.8 years, while on an average the age of patients admitted to the hospital is 35.37 years. Mode is less than the mean.

Question 2.
The following data gives the information on the observed life times (in hours) of 225 electrical components : (AS₄)

Lifetimes (in hours)	0 – 20	20 – 40	40 – 60	60 – 80	80 – 100	100 – 120
Frequency	10	35	52	61	38	29

Determine the modal life times of the components.
Solution:

Class interval	Frequencies
0-20	10
20-40	35
40-60	52
60-80	61
80 – 100	38
100 – 120	29

Since the maximum frequency 61 is in the class 60 – 80, this is the required modal class.
Modal class frequency, f₁ = 61
Frequency of the class preceding the modal class f₀ = 52
Frequency of the class succeding the modal class f₂ = 38
lower boundary of the modal class l = 60
Height of the class, h = 20
∴ Mode (z) = l + \(\frac{\left(f_1-f_0\right)}{2 f_1-\left(f_0+f_2\right)}\) × h
= 60 + \(\left[\frac{61-52}{2 \times 61-(52+38)}\right]\) × 20
= 60 + \(\frac{9}{122-90}\) × 20
= 60 + \(\frac{9}{32}\) × 20
= 60 + 5.625 = 65.625 hours.

Question 3.
The following data gives the distribution of total monthly household expenditure of 200 families of Gummadidala village. Find the modal monthly expenditure of the families. Also find the mean monthly expenditure. (AS₄)

Expenditure (in rupees)	1000-1500	1500-2000	2000-2500	2500-3000	3000-3500	3500-4000	4000-4500	4500-5000
Number of families	24	40	33	28	30	22	16	7

Solution:

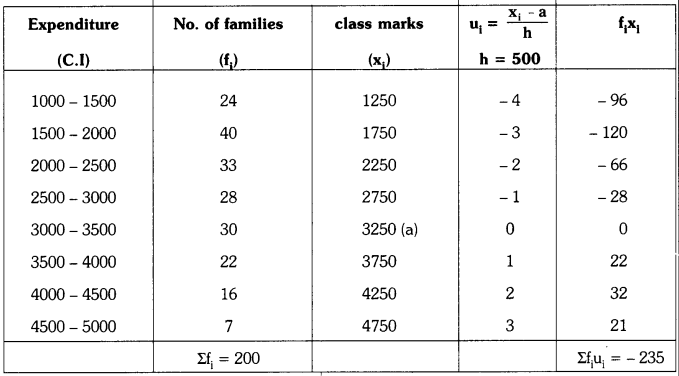
Assumed mean (a) = 3250
Σf_i = 200; Σf_iu_i = – 235
Mean monthly income = \(\overline{\mathrm{x}}\) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 3250 – \(\frac{235}{200}\) × 500
= 3250 – 587.5
= ₹ 2662.50
Since the maximum families 40 lies in the class 1500 – 2000, this is the required modal class.
Lower boundary of modal class (l) = 1500
Frequency of the modal class (f₁) = 40
Frequency of the class preceding the modal class f₀ = 24
Frequency of the class succeding the modal class f₂ = 33
Height of the class, h = 500
Mode (z) = l + \(\frac{\left(f_1-f_0\right)}{2 \times f_1-\left(f_0+f_2\right)}\) × h
⇒ 1500 + \(\frac{40-24}{2 \times 40-(24+33)}\) × 500
= 1500 + \(\frac{16 \times 500}{80-57}\) = 1500 + \(\frac{8000}{23}\)
⇒ 1500 + 347.826
= ₹ 1847.83
Hence, modal monthly income = ₹ 1847.83

Question 4.
The following distribution gives the state-wise, teachers, student ratio in higher second’ ary schools of India. Find the mode and mean of this data. Interpret the two measures. (AS₃, AS₄)

Number of students	15-20	20-25	25-30	30-35	35-40	40-45	45-50	50-55
Number of States	3	8	9	10	3	0	0	2

Solution:

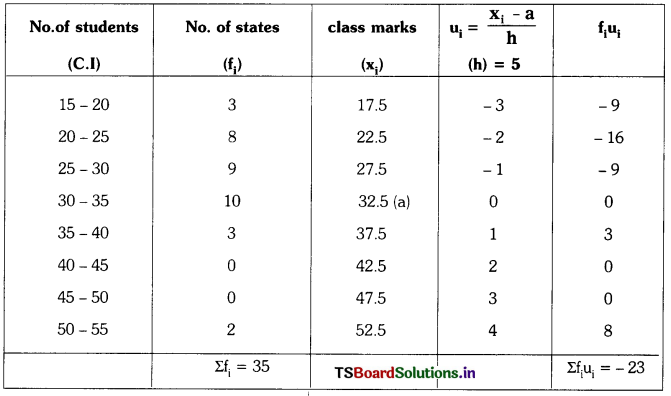
Mean (\(\overline{\mathrm{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
a – assumed mean = 32.5; h – height of the class = 5
∴ \(\overline{\mathrm{x}}\) = 32.5 – \(\frac{22}{35}\) × 5 = 32.5 – 3.28 = 29.22
Since the maximum number of states ‘10′ lies in the class interval 30 – 35, this is the modal class.
Lower boundary of the modal class, l = 30
Frequency of the modal class, f₁ = 10
Frequency of the class preceding the modal class, f₀ = 9
Frequency of the class succeding the modal class, f₂ = 3
Height of the class h = 5
Mode (z) = l + \(\left[\frac{f_1-f_0}{\left(f_1-f_0\right)+\left(f_1-f_2\right)}\right]\) × h
⇒ 30 + \(\frac{10-9}{(10-9)+(10-3)}\) × 5
= 30 + \(\frac{1 \times 5}{1+7}\) = 30 + \(\frac{5}{8}\)
= 30 + 0625 ⇒ 30.625.
Mode of states have a teacher students ratio 30.625 and on an average of this ratio is 29.22.

Question 5.
The given distribution shows the number of runs scored by some top batsmen of the world in one international cricket matches.

Runs	3000-4000	4000-5000	5000-6000	6000-7000	7000-8000	8000-9000	9000-10000	10000-11000
Number of batsmen	4	18	9	7	6	3	1	1

Find the mode of the data. (AS₄)
Solution:

Class interval	Frequencies
3000 – 4000	4
4000 – 5000	18
5000 – 6000	9
6000 – 7000	7
7000 – 8000	6
8000 – 9000	3
9000 – 10000	1
10000- 11000	1

Maximum no.of batsmen are in the class 4000 – 5000
Modal class is 4000 – 5000
Lower boundary of the modal class ‘l’ = 4000
frequency of the modal class, f₁ = 18
frequency of the class preceding the modal class f₀ = 4
frequency of the class succeeding the modal class f₂ = 9
Size of the class, h = 1000
Mode(z) = l + \(\left[\frac{\mathrm{f}_1-\mathrm{f}_0}{\left(\mathrm{f}_1-\mathrm{f}_0\right)+\left(\mathrm{f}_1-\mathrm{f}_2\right)}\right]\) × h
Mode (z) = 4000 + \(\frac{18-4}{(18-4)+(18-9)}\) × 1000
= 4000 + \(\frac{14}{14+9}\) × 1000
= 4000 + \(\frac{14000}{23}\) = 4000 + 608.695
= 4608.69
≅ 4608.7 runs

Question 6.
A student noted the number of cars passing through a spot on a road for 100 periods, each of 3 minutes and summarised this in the table given below.

Number of cars	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70	70 – 80
Frequency	7	14	13	12	20	11	15	8

Find the mode of the data. (AS₄)
Solution:

No.of cars	Frequency
0 – 10	7
10 – 20	14
20 – 30	13
30 – 40	12
40 – 50	20
50 – 60	11
60 – 70	15
70 – 80	8

Since, the maximum frequency is 20, the modal class is 40 – 50.
Lower boundary of the modal class, ‘l’ = 40
Frequency of the modal class, f₁ = 20
Frequency of the class preceding the modal class f₀ = 12
Frequency of the class succeeding the modal class f₂ = 11
Height of the class, h = 10;
Mode (z) = l + \(\left[\frac{\mathrm{f}_1-\mathrm{f}_0}{\left(\mathrm{f}_1-\mathrm{f}_0\right)+\left(\mathrm{f}_1-\mathrm{f}_2\right)}\right]\) × h
= 40 + \(\frac{(20-12)}{(20-12)+(20-11)}\) × 10
= 40 + \(\frac{8}{8+9}\) × 10
= 40 + \(\frac{80}{17}\)
= 40 + 4.70588
= 44.705
≅ 44.7 cars.