We are offering TS 10th Class Maths Notes Chapter 13 Probability to learn maths more effectively.
TS 10th Class Maths Notes Chapter 13 Probability
→ Probability :
Probability means the number of occasions that a particular statement (Or) event is likely to occur in a large population of events.
→ Random experiment:
Random experiments (or) tail is an act (or) process that leads to a result, that cannot be predicted in advance.
(or)
An experiment is said to be a random experiment if its outcome cannot be predicted. That is the outcome of an experiment does not obey any rule.
Ex:
(i) If a coin is tossed, we can’t say whether head or tail will appear. So tossing a coin is a random
experiment.
(ii) If we throw a die numbered 1,2,3,4,5,6 on its six faces, it is impossible to say which numbered face will appear. There is no rule to know it. So throwing a die is a random experiment.
![]()
→ Equally likely events :
Two or more events are said to be equally likely if each one of them has an equal chance of occurrence.
For example
- When a coin is tossed, the two possible outcomes, head and tail, are equally likely.
- When a die is thrown, the six possible outcomes, 1, 2, 3,4, 5 and 6 are equally likely.
→ Mutually exclusive events :
Two (or) more events are mutually exclusive if the occurrance of each event prevents the every other event.
→ Complementary events :
Consider an event has few outcomes. Event of all other outcomes in the sample survey which are not in the favourable event is called complementary event.
→ Exhaustive events :
All the events are exhaustive if their union is the sample space.
→ Sure events:
The sample space of a random experiments is called sure(or) certain event as any one of its elements will surely occur in any trail of experiment.
→ Impossible event:
An event which will not occur on any account is called an impossible event.
→ Theoretical event:
The theoretical (classical) probability of an event E, written as P(E), is defined as No. of trails in which the events happened
P(E) = \(\frac{\text { No. of trails in which the events happened }}{\text { Total number of trials }}\)
Where we assume that the outcomes of the experiment are equally likely.
→ Elementary event: An event having only one outcome is called an elementary event.
The sum of the probabilities of all the elementary events of an experiment is 1.
The probability of a sure (or certain event) is 1.
The probability of an impossible event is 0.
The probability of an event E is a number P(E) such that 0 < P(E) < 1.
For an event E, P(E) + P(Ē) = 1 where E stands for ‘not E’.
E and Ē are called complementary events. In general, it is true that for an event E,
P(Ē) = 1 – P(E)
![]()
→ Sample space : The set of all possible outcomes of an experiment is called a sample space (or) probability space.
Suppose we throw a die once. As it has six faces, every face has equal chance to appear.
Therefore, sample space (s) = {1, 2, 3, 4, 5, 6}
Number of events n(s) = 6
If a coin is tossed, either head (or) tail may appear.
Hence, sample space (s) = {H, T}
Number of events n (s) = 2
→ A cubic dice is a six faced cube, the six faces are marked as 1, 2, 3,4, 5, 6. When such a dice is thrown, any one of the faces come upwards. The number on this face is the outcome of the experiment.
→ Remember the following points :
(a) There are 52 cards in a pack of cards.
(b) Out of these, 26 are red and 26 are black.
(c) Out of 26 red cards, 13 are hearts and 13 are diamonds.
(d) Out of 26 black cards, 13 are spades and 13 are clubs.
(e) Each of four varities (hearts, diamonds, spades, clubs) has an ace (i.e.,) a pack of 52 cards has 4 aces.
Similarly these are 4 kings, 4 queens and 4 jacks.
Flow Chat:
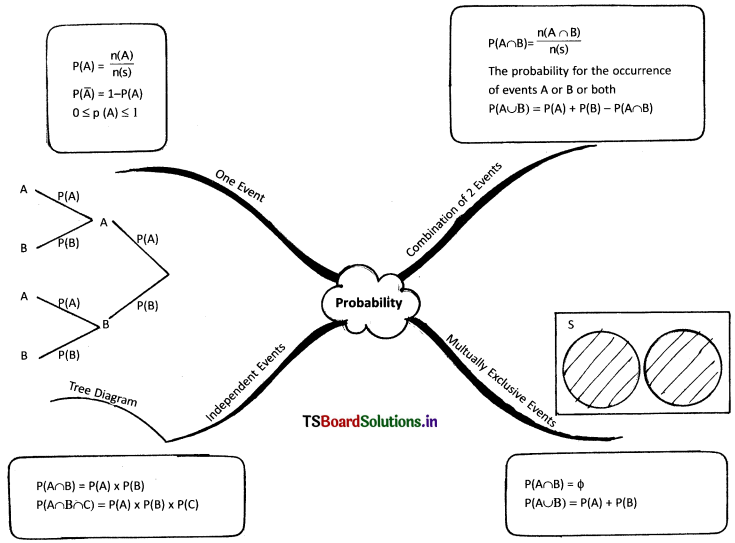
![]()
Pierre Simon Laplace:
- The definition of probability was given by Pierre Simon Laplace in 1795.
- Probability theory had its origin in the 16th Century, when an Italian physician and mathematician J.Cardan wrote the first book on the subject, “The Book on Games of Chance”.
- James Bernoulli (1654 – 1705), A. De Moivre(1667-1754) and Pierre Simon Laplace (1749-1827) are among those who made significant contributions to this field.
- In recent years, probability has been used extensively in many areas such as Biology, Economics, Genetics, Physics, Sociology etc.