TS Inter 1st Year Maths 1B Solutions Chapter 2 Transformation of Axes Ex 2(a)

Students must practice these TS Intermediate Maths 1B Solutions Chapter 2 Transformation of Axes Ex 2(a) to find a better approach to solving the problems.

TS Inter 1st Year Maths 1B Transformation of Axes Solutions Exercise 2(a)

I.
Question 1.
When the origin is shifted to (4, – 5) by the translation of axes, find the coordinates of the following points with reference to new axes. (V.S.A.Q.)
(i) (0, 3)
(ii) (-2, 4)
(iii) (4, -5)
Answer:
(i) (0, 3)
New origin = (4, -5) = (h, k)
Old co-ordinates are (0, 3) = (x, y)
x’ = x – h = 0 – 4 = – 4 and y’ = y – k = 3 + 5 = 8
∴ New coordinates = (- 4, 8)

(ii) (- 2, 4)
New origin = (4, -5) = (h, k)
Old coordinates are (- 2, 4) = (x, y)
x’ = x – h = – 2 – 4 = – 6
y’ = y – k = 4 + 5 = 9
∴ New coordinates = (- 6, 9)

(iii) (4, – 5)
New origin = (4, -5) = (h, k)
Old coordinates are (4, -5) = (x, y)
x’ = x – h = 4 – 4 = 0
y’ = y – k = – 5 + 5 = 0
∴ New coordinates = (0, 0)

Question 2.
The origin is shifted to (2,3) by the translation of axes. If the co-ordinates of a point P change as follows, find the co-ordinates of P in the original system. (V.S.A.Q.)
(i) (4, 5)
(ii) (-4, 3)
(iii)(0, 0)
Answer:
(i) (4, 5)
New coordinates (x’,y’) = (4, 5)
origin (h, k) = (2, 3)
Old coordinates of P are x = x’ + h = 4 + 2 = 6
y = y’ + k = 5 + 3 = 8
∴ Old coordinates = (6, 8)

(ii) (- 4, 3)
New coordinates (x’, y’) = (-4, 3)
origin (h, k) = (2, 3)
Old coordinates of P are x = x’ + h = – 4 + 2 = – 2
y = y’ + k = 3 + 3 = 6
∴ Old coordinates = (- 2, 6)

(iii) (0, 0)
New coordinates (x’,y’) = (0, 0)
origin(h, k) = (2, 3)
Old coordinates of P are x = x’ + h = 0 + 2 = 2
y = y’ + k = 0 + 3 = 3
∴ Old co-ordinates = (2, 3)

Question 3.
Find the point to which the origin is to be shifted so that the point (3,0) may change to (2, -3). (V.S.A.Q.)
Answer:
(x, y) = (3, 0)
(x’,y’) = (2,-3)
Let ( h, k ) be the shifted origin,
h = x – x’ = 3 – 2 = 1
k = y – y’ = 0 + 3 = 3
∴ (h, k) = (1, 3)

Question 4.
When the origin is shifted to (-1, 2) by the translation of axes, find the transformed equations of the following.
(i) x² + y² + 2x – 4y + 1 = 0
(ii) 2x² + y² – 4x + 4y = 0 (V.S.A.Q.)
Answer:
(i) x² + y² + 2x – 4y + 1 = 0
The given equation is
x² + y² + 2x – 4y + 1 = 0
origin is shifted to (-1, 2)
∴ h = – 1, k = 2
Transformed equations are
x = x’ + h, y = y’+ k
⇒ x = x’ – 1, y = y’ + 2
∴ The new equation is
(x’ – 1)² + (y’ + 2)² + 2( x’ – 1) – 4(y’ + 2) + 1 = 0
x’² + 1 – 2x’ + y’² + 4y’ + 4 + 2x ‘ – 2 – 4y’- 8 + 1 = 0
⇒ x’² + y’² – 4 = 0

(ii) 2x² + y² – 4x + 4y = 0
The given equation is
2x² + y² – 4x + 4y = 0
By the above transformation we have
x = x’ – 1, y = y’ + 2
∴ 2 (x’ – 1)² + (y’ + 2)² – 4(x’ – 1) + 4 (y’ + 2) = 0
⇒ 2 [ x’² – 2x’ + 1] + y’² + 4y’ + 4 – 4x’ + 4 + 4 y’ + 8 = 0
⇒ 2 x’² + y’² – 8x’ + 8y’ + 18 = 0

Question 5.
The point to which the origin is shifted and the transformed equations are given below. Find the original equation.
(i) ( 3, – 4 ) ; x² + y² = 4
(ii) (-1, 2 ) ; x² + 2y² + 16 = 0 (V.S.A.Q.)
Answer:
(i) ( 3, – 4 ) ; x² + y² = 4
Shifted origin = (h, k) = ( 3, – 4)
x’ = x – h
= x – 3
y’ = y – k
= y + 4
The given equation is x² + y² = 4
The original equation of 3x’² + y’² = 4 is
(x – 3)² + (y + 4)² = 4
⇒ x² – 6x + 9 + y² + 8y + 16 = 4
⇒ x² + y² – 6x + 8y + 21 = 0

(ii) (-1, 2) ; x² + 2y² + 16 = 0
Given shifted origin = (h, k) = (- 1, 2)
x’=x + h
= x + 1
y’ = y + k
= y – 2
The original equation of x’² +2 y’² + 16 = 0 is
( x + 1)² + 2 (y – 2)² + 16 = 0
⇒ x² + 2x + 1 + 2 ( y² – 4y + 4) + 16 = 0
⇒ x² + 2y² + 2x – 8y + 25 = 0

Question 6.
The point to which the origin is shifted and the transformed equations are given below.
Find the original equation.
(i) (3, – 4); x² + y² = 4
(ii) (- 1, 2); x² + 2y² + 16 = O (V.S.A.Q.)
Answer:
(3, – 4); x² + y² = 4
Shifted origin (h, k) = (3, – 4)
x’ = x – h
= x – 3
y’ = y – k
= y + 4
The given equation is x² + y² = 4
The original equation of 3x’² + y’² = 4 is
(x – 3)² + (y + 4)² = 4
⇒ x² – 6x + 9 + y² + 8y + 16 = 4
⇒ x² + y² – 6x + 8y + 21 = 0

(ii) (- 1, 2) ; x² + 2y² + 16 = 0
Given shifted origin = (h, k) = (- 1, 2)
x’ = x + h
= x + 1

y’ = y + k
= y – 2
The origin equation of x’² + 2y’² + 16 = 0 is
(x + 1)² + 2(y – 2)² + 16 = 0
⇒ x² + 2x + 1 + 2 (y² – 4y + 4) + 16 = 0
⇒ x² + 2y² + 2x – 8y + 25 = 0

Question 7.
Find the point to which the origin is to be shifted so as to remove the first degree terms from the equation 4x² + 9y² – 8x + 36y + 4 =0. (V.S.A.Q.)
Answer:
The given equation is
4x² + 9y² – 8x + 36y + 4 = 0
To make first degree terms missing in the equation origin should be shifted to \(\left(\frac{h f-b g}{a b-h^2}, \frac{g h-a f}{a b-h^2}\right)\)
Comparing with
ax² + 2hxy + by² + 2gx + 2fy + c = 0 we have
a = 4, b = 9, h = 0, g = – 4, f = 18, c = 4

Question 8.
When the axes are rotated through an angle 30°, find the new coordinates of the following points. (V.S.A.Q.)
(i) (0, 5)
(ii) (- 2, 4)
(iii) (0, 0)
Answer:
(i) ( 0, 5 )
Given θ = 30° and (x, y) = (0, 5)
We have x’ = x cos θ + y sin θ
= 0 (cos 30°) + 5 ( sin 30°) = 5\(\left(\frac{1}{2}\right)\) = \(\frac{5}{2}\)
y’ = – x sin θ + y cos θ
= – 0 (sin 30°) + 5 cos 30° = \(\frac{5 \sqrt{3}}{2}\)
∴ New coordinates = \(\left(\frac{5}{2}, \frac{5 \sqrt{3}}{2}\right)\)

(ii) (-2, 4)
θ = 30° and (x, y) = (-2, 4)
We have x’= x cos θ + y sin θ
= – 2 cos 30° + 4 sin 30°
= – 2 \(\left(\frac{\sqrt{3}}{2}\right)\) + 4\(\left(\frac{1}{2}\right)\) = – √3 + 2
y’ = – x sin θ + y cos θ
= – (- 2) sin 30° + 4 cos 30°
= 2 sin 30° + 4 cos 30°
= 2 \(\left(\frac{1}{2}\right)\) + 4 \(\left(\frac{\sqrt{3}}{2}\right)\) = 1 + 2√3
∴ New coordinates = (- √3 + 2, 1 + 2√3)

(iii) (0, 0)
θ = 30° and (x, y) = (0, 0)
x’= x cos θ + y sin θ
= 0 cos 30° + 0 sin 30° = 0
y’ = – x sin 0 + y cos 0
= – (0) sin 30° + 0 cos (30°) = 0
∴ New coordinates = (0, 0)

Question 9.
When the axes are rotated through an angle 60°, the new coordinates of three points are the following
(i) (3, 4)
(ii) (- 7, 2)
(iii) (2, 0)
Find their original coordinates. (V.S.A.Q.)
Answer:
Given θ = 60°, (x’, y’) = (3, 4)
We have x = x’ cos θ – y’ sin θ
= 3 cos 60° – 4 sin 60°

(ii) Given θ = 60° and (x’, y’) = (-7, 2)
We have x = x’ cos θ – y’ sin θ
= (- 7) cos 60° – 2 sin 60°

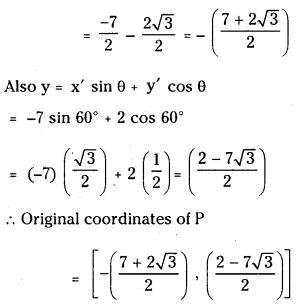
(iii) Given θ = 60°; (x’, y’) = (2, 0)
We have x = x’ cos θ – y’ sin θ
= 2 cos 60° – 0 sin 60°
= 2\(\left(\frac{1}{2}\right)\) – 0 \(\left(\frac{\sqrt{3}}{2}\right)\) = 1
Also y = x’ sin θ + y’ cos θ
= 2 sin 60° + 0 cos 60° = √3
= 2\(\left(\frac{\sqrt{3}}{2}\right)\) + 0\(\left(\frac{1}{2}\right)\) = √3
∴ Original coordinates of P = (1, √3)

Question 10
Find the angle through which the axes are to be rotated so as to remove the xy term in the equation x² + 4xy + y² – 2x + 2y – 6 = 0. (V.S.A.Q.) (June 2004)
Answer:
Comparing the given equation with
ax² + 2hxy + by² + 2gx + 2fy + c = 0
We have a = 1, 2h = 4 ⇒ h = 2,
b = 1, 2g = – 2 ⇒ g = – 1
2f = 2 ⇒ f = 1, c = – 6
Let θ be the angle of rotation of axes, then

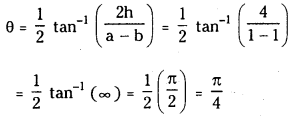
II.
Question 1.
When the origin is shifted to the point (2, 3), the transformed equation of a curve is x² + 3xy – 2y² + 17x – 7y – 11 = 0. Find the original equation of the curve. (S.A.Q.) (March 2011)
Answer:
Transformed equations are

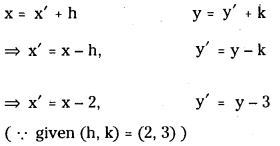
Transformed equation is
x’² + 3x’y’ – 2 y’² + 17x’ – 7y’ – 11 = 0
Original equation is
(x – 2)² + 3 (x – 2) (y – 3) – 2 (y – 3)² – 7 (y – 3) – 11 = 0
⇒ x² – 4x + 4 + 3 (xy – 2y – 3x + 6) – 2 (y² – 6y + 9) – 7y + 21 – 11 = 0
⇒ x² + 3xy – 2y² + 4x – y – 20 = 0
∴ The original equation of the curve is
x² + 3xy – 2y² + 4x – y – 20 = 0

Question 2.
When the axes are rotated through an angle 45°, the transformed equation of a curve is 17x² – 16xy + 17y² = 225. Find the original equation of the curve. (S.A.Q.) (May 2012)
Answer:
Angle of rotation is θ = 45°
x’ = x cos θ + y sin θ
= x cos 45° + y sin 45°
= x\(\left(\frac{1}{\sqrt{2}}\right)\) + y\(\left(\frac{1}{\sqrt{2}}\right)\) = \(\frac{x+y}{\sqrt{2}}\)
y’ = – x sin θ + y cos θ
= – x sin 45° + y cos 45°
= – \(\frac{x+y}{\sqrt{2}}\)
The original equation of the curve
⇒ 17x² – 16x’y + 17y’² = 225 is

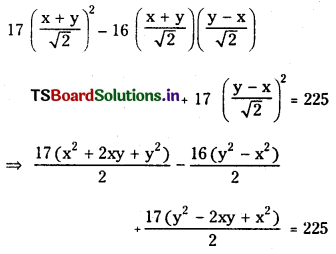
⇒ 17x² + 17y² + 34xy – 16y² + 16x² + 17x² + 17y² – 34xy = 450
⇒ 50x² + 18y² = 450
⇒ 25x² + 9y² = 225

Question 3.
When the axes are rotated through an angle a, find the transformed equation of x cos α + y sin α = p. (S.A.Q.) (Mar. ’14, May 2007)
Answer:
Given equation is x cos α + y sin α = p and axes are rotated through an angle α.
x = x’ cos α – y’ sin α
y = x’ sin α + y’ cos α
The given equation transformed to
(x’ cos α – y’ sin α) cos α + ( x’ sin α + y’ cos α) sin α = p
⇒ x’ (cos²α + sin²α) = p
⇒ x’ = p
∴ Transformed equation is x = p.

Question 4.
When the axes are rotated through an angle \(\frac{\pi}{6}\), find the transformed equation of x² + 2 √3 xy – y² = 2a². (S.A.Q.) (March 2012, ’07, 04; May 2006 )
Answer:

⇒ 3x² – 2√3 + y² + 6x² – 2√3 xy + 6√3 xy – 6y² – x² – 2√3 xy – 3y² = 8a²
⇒ 8x² – 8y² = 8a²
⇒ x² – y² = a²
∴ Required transformed equation is x² – y² = a²

Question 5.
When the axes are rotated through an angle \(\frac{\pi}{4}\), find the transformed equation of
3x² + 10xy + 3y² = 9. (S.A.Q.) (May’14, ’11)
Answer:
Given equation is
3x² + 10xy + 3y² = 9 …………… (1)
and angle of rotation θ = \(\frac{\pi}{4}\)
Let (X ,Y) be the new coordinates of (x, y) then x = X cos θ – Y sin θ

⇒ 3X² – 6XY + 3Y² + 10X² – 10Y² + 3X² + 6XY + 3Y² = 18
⇒ 16X² – 4Y² – 18 = 0
⇒ 8X² – 2Y² = 9
∴ The transformed equation of the given equation is
8X² – 2Y² = 9