TS Board TS 6th Class Science Study Material Pdf 13th Lesson Learning How to Measure Textbook Questions and Answers.
Learning How to Measure – TS 6th Class Science 13th Lesson Questions and Answers Telangana
Improve Your Learning
Question 1.
What is the smallest distance that you can measure with a centimeter scale ? (Conceptual Understanding) 2 M
Answer:
- The smallest distance that we can measure with a centimeter scale is ‘one millimeter’ (1 mm).
- 1 centimeter = 10 millimeters or 1 cm – 10 mm
![]()
Question 2.
Are we able to measure the thickness of a metal wire using a scale ? Explain. (Conceptual Understanding) 2 M
Answer:
- It is not possible to measure the thickness of a metal wire using a scale.
- The smallest length we can measure with a centimeter scale is “one millimeter.
- We cannot measure “fraction of a millimeter.
Question 3.
A school hall measures 20 m in length and 15 m in breadth. Find its area. (Conceptual Understanding) 2 M
Answer:
Length of school hall (l) = 20 m
Breadth of school hall (b) = 15 m
Area of school hall (A) = lengh × breadth (l × b)
= 20 m × 15 m
∴ A = 300 m2 = 300 sq.m
Question 4.
Ramu’s father had a rectangular plot of length 60 ft and breadth 50 ft. He built a house occupying length 40 ft of the plot and breadth 40 ft and in the remaining area he planned a garden. Can you help Ramu to find out the area of his garden? (Conceptual Understanding) 2M
Answer:
length of garden = length of the plot – length of house
= 60 ft – 40 ft = 20 ft.
Breadth of garden = breadth of the plot – breadth of house
= 50 ft – 40 ft = 10 ft.
Area of his garden = length x breadth
= 20 ft x 10 ft = 200 ft2.
Question 5.
Match the following (Conceptual Understanding) 2M
Answer:
| A | B | ||
| (a) liter | 2 | 1) 10000 m2 | |
| (b) A meter | 3 | 2) 1000 ml | |
| (c) A kilometer | 4 | 3) 100 cm | |
| (d) A centmeter | 5 | 4) 1000 m | |
| (e) 1 hectare (nearly 2.5 Acres) | 1 | 5) 10 mm |
Question 6.
Milliliter is a unit for measuring …………….. (Conceptual Understanding) 2M
Answer:
Volume
Question 7.
For measuring long distances we can use …………… as a unit. (Conceptual Understanding) 2M
Answer:
Kilometer
![]()
Question 8.
What method will you adopt to measure the volume of a banana ? Explain. (Experimentation andfield investigation) 4 M
Answer:
Banana has an irregular shape. So I follow the method, “to measure volume of irregular solids using a measuring cylinder”.
Explanation:
- A measuring cylinder is taken.
- It is half – filled with water.
- The volume of water is recorded. It is, ‘a’ ml.
- The banana is tied with a fine cotton thread.
- The banana is gently put in the water so that it is completely immersed in water.
- The level of water in the cylinder rises.
- The new volume of water is recorded. It is, ‘b’ ml.
∴ Volume of the banana = b ml – a ml = (b – a) ml.
Question 9.
Identify incorrect statements among the following and rewrite them with necessary corrections : (Asking questions and making hypothesis) 8M
a) One square meter is equal to 100 square centimeters
b) The appropriate unit for reporting the volume of a cylindrical rod is cm2, (square centimeter)
c) The appropriate instrument to measure the thickness of a 25 paise coin is tailor’s tape
d) A measuring cylinder can directly measure the volume of solids.
Answer:
| Given statement | Corrected statement |
| a) One square meter is equal to 100 square centimeters | 1. 1 m2 = 10,000 cm2
meter x meter = 100 cm x 100 cm, m2 = 10,000 cm2
2. ∴ One square meter is equal to ten thousand square centimeters. |
| b) The appropriate unit for reporting the volume of a cylindrical rod is cm2, (square centimeter) | b. The appropriate unit for reporting the volume of a cylindrical rod is cm3, (cubic centimeter) |
| c) The appropriate instrument to measure the thickness of a 25 paise coin is a tailor’s tape | (c) Wrong.
1. A number of these coins (say, 10) are placed one upon the other. 2. The total thickness is measured with a scale. 3. It is divided by the no. of coins. 4. Then we get the thickness of single coin. |
| d) A measuring cylinder can directly measure the volume of solids. | d. No. We require a measuring cylinder and a liquid in which the given solid doesn’t dissolve. (For details, refer Q. 8) |
Question 10.
How will you measure the area of your palm using graph paper ? Explain.
Answer:
Our palm is measured by using a graph paper.
Method of finding the area of palm using a graph paper: (Experimentation andfield investigation) 8M
- Palm is placed on a graph paper.
- The boundary of the palm is marked on a graph paper.
- Palm is removed. We have the outline or boundary of the palm on the graph paper.
- The number of complete squares (each of 1 cm2 area) lying inside the boundary are counted.
- Also, those squares lying inside the boundary, which are half or greater than half are counted.
- This is added to the number of complete squares.
- This total number gives the area of the palm. If this number is n, Area of palm = n cm2
![]()
Question 11.
Measure the volume of “Kalakanda” (sugar crystal) and piece of “Patika” (alum) – Record your measurements in given table 8M
Answer:
| Name of the student | Volume of Kalakanda | Volume of Patika |
| – | – | – |
| – | – | – |
| – | – | – |
| – | – | – |
a) Are all the volumes of Kalakanda equal ?
b) Are all the volumes of Patika equal ?
c) If not, state the possible reasons.
Ask your friends to measure volumes of the same pieces of Kalakanda and Patika and record the values .(Experimentation andfield investigation)
Answer:
1. Both Kalakanda and Patika are soluble in water. So water can’t be used in the measuring. Both are insoluble in liquids like kerosene. So kerosene is used.
2. Their volumes are found, from the volume of kerosene displaced by them in a measuring cylinder.The values are tabulated as under.
| Name of the student | Volume of Kalakanda | Volume of Patika |
| Kartik | 28.9 cm3 | 26.4 cm3 |
| Deepu | 28.8 cm3 | 26.5 cm3 |
| Rahim | 30.0 cm3 | 26.5 cm3 |
| Sitalu | 30 cm3 | 26.4 cm3 |
(a) No
(b) No
(C) Possible reasons are :
1) In the measuring Jar, we have to read the marking at the lowest point of the concave surface of liquid. For that, we must bring our eyes in line with this level and then read it. If this procedure is not followed well, we get error while noting the reading.
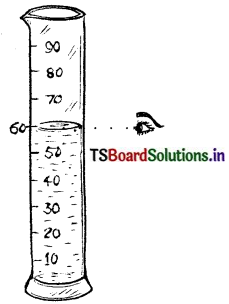
2) Human error, while taking down the reading on paper.
3) These two substances are not hard like stones. They are brittle. So naturally some amount of it gets lost, as many students handle them.
![]()
Question 12.
A carpenter who makes wooden furniture needs accuracy in measurements. Do you ever notice how he measures ? How would you appreciate him? (Appreciation and Aesthetic sense and values) 4M
Answer:
- As the carpenter is a practical worker. He always be cautious on measuring the wood.
- Carpenter takes measurements very accurately and nearest to a millimeter.
- He puts his mind on the job and concentrates on the measurements to design beautiful furniture.
- Carpenters mostly depend on a right angled strip, a steel tape, pencil etc., to measure the wood.
Question 13.
Make a visit to panchayat office. Collect information, how VRO measure areas of agricultural lands in your village. Prepare a questionnaire for this. (Information skills and projects) 4 M
- The panchayat office VRO uses metal chain tape to mark the boundaries of house land or agricultural fields.
- The measuring chains are made in links.
- It is not possible to measure the largest fields with tape. So these metal chain made tapes are used.
Questionnaire:
- What is the advantage of using chain instead of tape ?
- Is it accurate to measure the fields with metal chain ?
- Are there any measuring devices other than metal chain ?
Question 14.
Collect any Invitation card with envelope. Find out the difference between measurements of card and cover. Write down the process that you follow. (Experimentation andfield investigation) 4M
Answer:
- The cover is put on a flat surface (a table)
- A metre scale is taken.
- The scale is placed exactly along the length of the cover.
- Zero point on the scale is made to coincide with the starting point of the cover.
- The eye is placed vertically above the point of coincidence of scale where the measurement is to be taken.
- The length of the cover is measured more than two times. Then the average reading is taken. A similar procedure is followed to find the breadth of the cover. It is found that, the length and breadth of the card are slightly less than those of the cover.
![]()
Question 15.
The distance between numbers in a clock is accurately same. List out the things that you observe in your surroundings with accurate distance between them. (Information skills and projects) 4M
Answer:
There are number of things in our surroundings with accurate distance between them. Some of them are :
- Pillars in a common hall
- Iron rods in a window
- Floor – designing
- Wings of a fan
- Stripes on a cloth
- Pillars in a compound wall, etc.
Question 16.
Try to imagine the area of CD, sim card, mobile phone, then find out the area of the above by using graph paper. Compare the values of your guess with graph paper measurement. Which thing is closely related to your guess?
Answer:
Area of mobile phone. It is rather easier to guess the length and breadth of a mobile phone, which has a rectangular shape and is medium in size.
TS 6th Class Science 13th Lesson Notes – Learning How to Measure
- Palm, Hand-span, foot-span, cubit, and stride are some conventional methods used earlier to measure lengths and small distances.
- The above conventional unit of measurement is not accurate. Because the length of the unit changes from person to person.
- The system of units now used is known as the International system of units (SI units).
- ‘Meter’ is the standard unit for measuring length.
- Meter scale is a standard instrument to measure length.
- Large distances can be measured in kilometers.
- Area is the measure of the extent of plane surface occupied by an object.
- Generally we measure area in square meters or square centimeters etc.
- Volume is a measure of the extent of space occupied by a body.
- Volumes of liquids can be measured using measuring cylinders.
- A measuring cylinder is marked from bottom to the top.
- Volume of liquids is measured in litres or milliliters.
- Volume of solids is measured in cubic meters, cubic centimeters, etc.
- Using a measuring cylinder and a liquid (Ex: water), we can measure the volume of an irregular solid.
- Measure : The comparison of an unknown quantity with some known quantity is said to be measurement.
- Standard Unit : Internationally accepted unit is called standard unit and internationally accepted instrument is called standard instrument. Eg: Gram, litre, metre.
- Area : Area is a measure of the extent of the plane surface occupied by an object. Area is measured in square meters or square centimeters.
- Volume : Volume is a measure of the extent of space occupied by a body. Volume of solids is measured in cubic meters, or cubic centimeters. Volume of liquids is measured in litres or millilitres.
- Regular surface : If body is in regular shape like square, rectangle then the surface of the body is said to be regular surface.
- Irregular surface : 11 body is in irregular shape like banana peel or leaf, then the surface of the body is said to be irregular surface.
- Measuring cylinder: It is a specially designed instrument for measuring volume of liquids such as water, milk, etc.
- Graph paper It is a paper that has small squares printed on it, so that we can use it for drawing graphs.