We are offering TS 10th Class Maths Notes Chapter 3 Polynomials to learn maths more effectively.
TS 10th Class Maths Notes Chapter 3 Polynomials
→ Polynomials are algebraic expressions constructed using constants and variables.
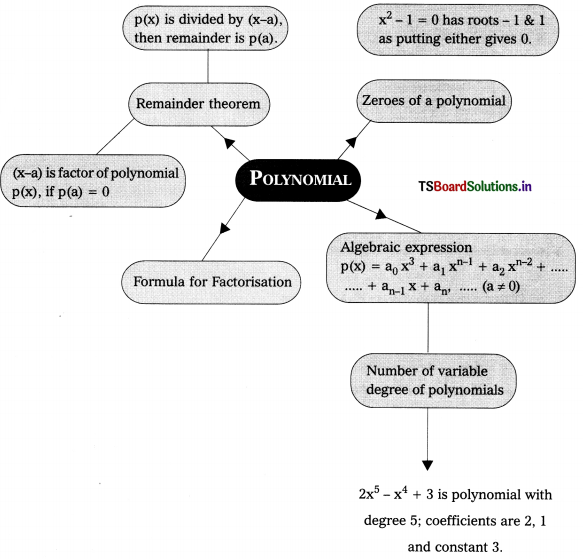
→ If p(x) is a polynomial in x, the highest power of x in p(x) is called the degree of the polynomial p(x).
→ Zero polynomial: A polynomial of degree zero is called zero polynomial.
E.g.: f(x) = 8,
g(x) = \(\frac{-5}{8}\)
→ Linear polynomial: A polynomial of degree ‘1’ is called linear polynomial.
E.g.: f(x) = 3x + 5, g(y) = 7y – 1, h(z) = 5z – 3
→ Quadratic polynomial: A polynomial of degree ‘2’ is called a quadratic polynomial.
E.g.: f(x) = 5x2, f(x) = 7x2 – 5x, f(x) = 6x2 – 7x + 5
→ Cubic polynomial: A polynomial of degree ‘3’ is called a cubic polynomial.
E.g.: f(x) = 5x3 + 4x2 – 3x + 6
![]()
→ Polynomial of degree ‘n’ in Standard Form : A polynomial in one variable Y of degree ‘n’ is an expression of the form.
F(x) = a0xn + a1xn-1 + a2xn-2 + ………… + an-1x + an, where a0, a1 , an are real coefficients and a ^ 0.
→ A real number k is said to be a zero of a polynomial p(x), if p(k) = 0.
→ The zero of the linear polynomial ax + b is \(\frac{-b}{a}\).
→ If a and P are the zeroes of the quadratic polynomial ax2 + bx + c then
- α + β = \(\frac{-b}{a}=\frac{-(\text { Coefficient of } x)}{\text { Coefficient of } x^2}\)
- αβ = \(\frac{c}{a}=\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)
→ Division Algorithm : Dividend = Divisor × Quotient + Remainder.
→ Value of a polynomial at a given point: If p(x) is a polynomial in x and a is real number then the value obtained by putting x = a in p(a) is called the value of p(x) at x = a.
E.g.: Let p(x) = 5x2 – 4x + 2, then its value at x = 2 is given by
p(2) = 5(2)2 – 4(2) + 2 = 5(4) – 8 + 2 = 20 – 8 + 2 = 14
Thus, the value of p(x) at x = 2 is 14.
→ Graph of a polynomial: In algebraic or in set theory language, the graph of a polynomial f(a) is the collection (or set) of all points (a, y) where y = f(x)
- Graph of a linear polynomial ax + b is a straight line.
- The graph of quadratic polynomial (ax2 + bx + c) is U – shaped, called Parabola.
- If a > 0 in ax2 + bx + c, the shape of parabola is opening upwards ‘U’.
- If a < 0 in ax2 + bx + c, the shape of parabola is opening downwards ‘n’.
→ How to make a quadratic polynomial with the given zeroes : Let the zeroes of a quadratic polynomial be α & β.
x = α, x = β
Then, obviously the quadratic polynomial is (x – α)(x – β) i.e., x2 – (α + β) x + aβ i.e., x2 – (sum of the zeroes) x + product of the zeroes.
→ Some useful relations :
- α2 + β2 = (α + β)2 – 2αβ
- (α – β)2 = (α + β)2 – 4αβ
- α2 – β2 = (α + β)(α – β) = (α + β) \(\sqrt{(\alpha+\beta)^2-4 \alpha \beta}\)
- α3 + β3 = (α + β)3 – 3αβ (α + β)
- α3 – β3 = (α – β)3 + 3αβ (α – β)
→ If α, β, γ are the zeroes of the cubic polynomial ax3 + bx2 + cx + d = 0 then
- α + β + γ = \(\frac{-b}{a}\)
- αβ + βγ + γα= \(\frac{c}{a}\)
- αβγ = \(\frac{-d}{a}\)
![]()
Important Formula:
- α + β = \(\frac{-b}{a}=\frac{-\text { coefficient of } x}{\text { coefficient of } x^2}\)
- αβ = \(\frac{c}{a}=\frac{\text { constant term }}{\text { coefficient of } x^2}\)
- Dividend = Divisor × Quotient + Remainder
- α + β + γ = \(\frac{-b}{a}\)
- αβ + βγ + γα = \(\frac{c}{a}\)
- αβγ = \(\frac{-d}{a}\)
Flow Chart
Ex.: (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx.
(x + y)3 = x3 + y3 + 3xy (x + y)
(x – y)3 = x3 – y3 – 3xy (x – y)
(x3 + y3 + z3 – 3xyz = (x + y + z) (x2 + y2 + z2 – xy – yz – zx)
Pavuluri Mailana (11th Century):
- Pavuluri Mailana of 11th century A.D. was a mathematician – poet of repute, who wrote his magnum opus in Telugu (Prosodical form) and named it Sarasangraha Ganitham.
- Sarasangraha Ganitham Mailana, it seems wrote 10 chapters, but only three chapters are available. These contains mostly arithmetic and some elementary algebra dealing with linear and quadratic equations.