TS 10th Class Maths Notes Chapter 10 Mensuration

We are offering TS 10th Class Maths Notes Chapter 10 Mensuration to learn maths more effectively.

TS 10th Class Maths Notes Chapter 10 Mensuration

Cuboid :

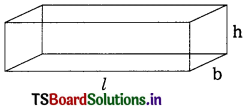
l, b and h denote respectively the length, breadth and height of a cuboid then

• Lateral surface area = 2h(l + b)
• Total surface area = 2(lb + bh + hl)
• Volume = lbh
• Diagonal of the cuboid = \(\sqrt{l^2+b^2+h^2}\)

Cube :

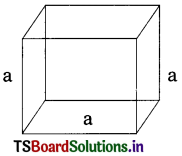
If the length of each edge of cube is “a” units then

• Lateral surface area = 4a²
• Total surface area = 6a²
• Volume = a³
• Diagonal of the cube = √3 × a = a√3

Right Prism :

• Lateral surface area = Perimeter of base × height
• Total Surface area = Lateral Surface area + 2(Area of end Surface)
• Volume = Area of base × height

Right Circular Cylinder:

If r is the radius of the base and ‘h’ is the height, then

• Lateral surface area = 2πrh
• Total surface area = 2πr(h + r)
• Volume = πr²h

Right Pyramid :

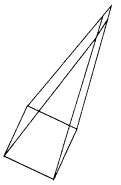
• Lateral surface area = \(\frac{1}{2}\) × perimeter of base × slant height
• Total Surface area = Lateral surface area + area of base
• Volume = \(\frac{1}{3}\) × area of base × height

Right Circular Cone :

If ‘r’ is the radius of the base, ‘h’ is the height and is slant height, then

• Lateral surface area = πrl.
• Total Surface area = πr(l + r)
• Volume = \(\frac{1}{3}\)πr²h
• l² = h² + r²

Sphere :

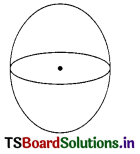
If ‘r’ is radius of sphere, then

• Lateral surface area = 4πr²
• Total surface area = 4πr²
• Volume = \(\frac{4}{3}\) πr³

Hemisphere :

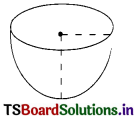
If Y is the radius of hemi-sphere, then

• Lateral surface area = 2πr²
• Total surface area = 3πr²
• Volume = \(\frac{4}{3}\)πr³

Right Circular Hollow Cylinder:

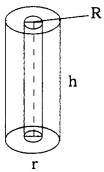
• Area of each end = π(R² – r²)
• Curved surface area of hollow Cylinder = External area + Internal area
  = 2πrh + 2πRh = 2πh(R + r)
• Total surface area = 2πRh + 2πrh + 2(πR² – πr²)
  = 2πh(R + r) + 2π(R + r)(R – r)
  = 2π(R + r) (R + h – r)
• Volume of the material = External volume – Internal volume
  = πR²h – πr²h = 7th(R² – r²)

Spherical Shell:

If R and r are the outer and inner radii of a spherical shell, then

• Outer surface area = 4πR²
• Volume of material = \(\frac{4}{3}\) π

→ The volume of the solid-formed by joining two basic solids is the sum of the volumes of the constituents.

→ In calculating the S.A of a combination of solids, we cannot add the surface area of the two constituents, because some part of the surface area disappears in the process of joining them.

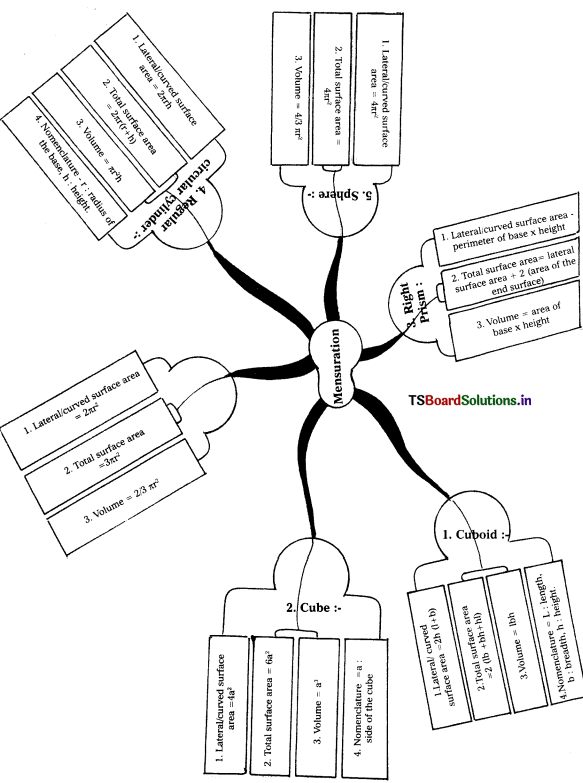
Flow Chat:

Brahmagupta (598 – 668):

• Brahmagupta was born in the state of Rajasthan.
• He worked in the great astronomical centre of ancient India – Ujjain.
• He made significant contributions to Trigonometry.