TS 10th Class Maths Notes Chapter 1 Real Numbers

We are offering TS 10th Class Maths Notes Chapter 1 Real Numbers to learn maths more effectively.

TS 10th Class Maths Notes Chapter 1 Real Numbers

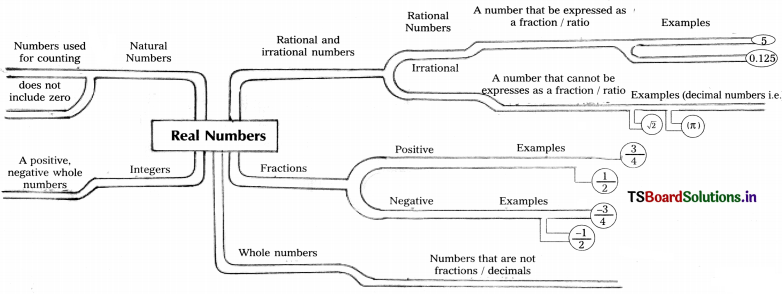
→ Set of Natural numbers N = {1, 2, 3, 4, ………………..}

→ Set of whole numbers W = {0, 1, 2, 3, …………..}

→ Set of Integers I or Z = {…………….., -3, -2, -1, 0,1, 2, 3,…………….}

→ Numbers that are of the form \(\frac{p}{q}\) where p and q are integer and q ≠ 0 are called Rational numbers they are denoted by Q.

→ Set of Rational numbers Q = {x/x = \(\frac{p}{q}\) where p, q ∈ Z, q ≠ 0}.

→ The set of Rational numbers is bigger set than integers.

→ All Rational numbers can be written either in the form of terminating decimals (or) non-terminating repeating decimals.

→ Numbers which cannot be expressed in the form of \(\frac{p}{q}\) when p, q are integers and q ≠ 0 are irrational numbers. Set of irrational numbers Q’ (or) ‘S’ = {√2, √3, √5, \(\frac{\sqrt{7}}{3}, \frac{1}{\sqrt{2}}, \frac{\sqrt{11}}{\sqrt{5}}\)}

→ π is an irrational number.

→ Irrational numbers are written as decimals. They are non-terminating, non-recurring.
Ex : √2 = 1.41421356 ; √1 = 3.14159

→ Set of rational and irrational numbers together called Real numbers.

→ Set of real numbers ‘R’ = Q ∪ Q’

→ All natural numbers except ‘1’ can be written as a product of their prime factors.
Ex: 3 = 3; 6 = 2 × 3; 253 = 11 × 23.

→ 1 is neither a composite nor a prime.

→ Every composite number can be written as the product of power of primes.

→ Fundamental theorem of Arithmetic : Every composite number can be expressed as the product of primes and this factorisation is unique, apart from the order in which prime factors occur.

→ Expressing a given number as the product of prime factors is called ‘prime factorisation.’

→ Let x be a rational number whose decimal expansion terminates, then x can be expressed in the form of \(\frac{p}{q}\) where p and q are co-primes and the prime factorisation of q is of the form 2n5m where m, n are non-negative integers.
Ex: \(\frac{7}{80}=\frac{7}{2^4 \times 5}=\frac{7 \times 5^3}{2^4 \times 5 \times 5^3}=\frac{7 \times 5^3}{2^4 \times 5^4}\) = 0.0875

→ Let x = \(\frac{p}{q}\) be a rational number such that the prime factorisation of q is not of the form 2ⁿ5^m where n, m are non-negative integers, Then x has a decimal expansion which is non-terminating repeating (recurring).
Ex : \(\frac{1}{7}\) is a non-terminating and recurring decimal because the denominator is 7 is not of the form 2n5m.
\(\frac{1}{7}\) = 0.1428571428571 = 0.142857

→ Let ‘P’ be a prime number. If p divide a² where ‘a’ is a positive integer then p divides ‘a’.

→ 2m general it can be shown that ^d is irrational when ever d is a positive integer which is not square of an integer.

→ The sum or difference of rational and an irrational number is irrational.

→ The product and quotient of a non-zero rational and irrational number is irrational.

→ Sum of the two irrational numbers need not to be irrational. The product of two irrational numbers need not be a irrational. Logarithms are used for all parts of calculation in engineering science, business and economics.

Laws of exponents :

• a^m × aⁿ = a^m+n
• a^m ÷ aⁿ = a^m-n
• a⁰ = 1

In general we write log_ax = n. If aⁿ = x where a and x are positive numbers and a ≠ 1.
x = aⁿ ⇒ log_ax = n (logarithm form)
log_ax = n ⇒ aⁿ = x (exponential form)

Laws of logarithms:

• log_axy = log_ax + log_ay
• log_a\(\frac{x}{y}\) = log_ax – log_ay
• log_ax^m = m log_ax

Note :

• log_a^a = 1
• log_a¹ = 0
• a_a^logm = m

→ Two natural numbers which do not have a common prime factor are called co-prime. Ex : (3, 4), (16, 25)

→ Prime numbers that differ by 2 are called Twin primes.
Ex : 17, 19; 29, 31

Important Formula:

• log_a xy = log_ax + log_ay
• log_ax/y = log_ax – log_ay
• a^log_aN = N
• log_a x^m = m log_ax
• a^x = N Then x = log_a^N

Flow Chat:

William Rowan Hamilton:

• William Rowan Hamilton was an Irish mathematician, physicist and astronomer who made important contributions to the development of optics, dynamics and algebra. His discovery of quaternions is perhaps his best known investigation.
• Dr. Brinkely remarked of Hamilton at the age of eighteen : “This young man, I do not say will be, but is, the first mathematician of his age.”